Runners in a race, probability paradox

[cosmicminer]

There are a number n of runners in a race.
We know their expected times from start to finish μ(i) and the corresponding standard deviations σ(i).
The probability of runner 0 to finish first is given by this integral:

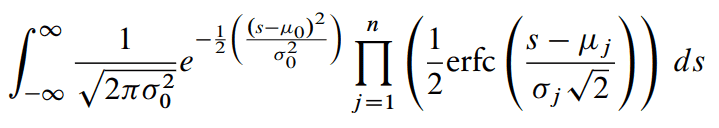
It's from here:

https://www.untruth.org/~josh/math/normal-min.pdf

The 0 is one of the i's really but is suffixed as 0 in the above image of the formula.
I would write i instead of "0" and then in the product j ≠ i rather.

This can be computed easily using Simpson's rule and the approximation for erfc from Abramowitz-Stegun perhaps.

The strange thing is this:
If I choose n = 2 and any values for μ and σ then the following holds true:

if μ(1) < μ(2) then always P(1) > P(2) irrespective of the σ's ................. (1)

This is a property of the double normal distribution.
Thus if runner 1 has a delta function for a distribution (limiting normal with σ = 0) and runner b is close second but with big σ then the 1 has higher probability irrespective.

But if n > 2 the law (1) may or may not hold - depending on the sigmas.
So for n > 2 it is possible that one of the theoretically faster runners has lower probability than a slower runner with bigger σ.
How is this possible ?

 

[mjc123]

It's not just about being faster than each rival in a pairwise comparison, but about being faster than all of them simultaneously. Thus if (because of the sigmas) there are several with a significant probability of beating the one with lowest μ, that one may not be the most likely to finish first.

Consider an extension of your example: 3 runners, A, B and C. A has a delta function, while B and C have identical (but independent) distributions with μ and σ such that the probability of B finishing after A is 55%.
The probability of A winning is the probability that both B and C finish later, i.e. 0.55² ≈ 0.3.
The probability that at least one of B and C finishes before A is 0.7.
By the symmetry of the situation, P(B) = P(C) = 0.35.
So A is more likely to beat B than B is to beat A, likewise with A and C. But B and C are each more likely to finish first of the 3 than A.

 

[cosmicminer]

It's not just about being faster than each rival in a pairwise comparison, but about being faster than all of them simultaneously. Thus if (because of the sigmas) there are several with a significant probability of beating the one with lowest μ, that one may not be the most likely to finish first.

Consider an extension of your example: 3 runners, A, B and C. A has a delta function, while B and C have identical (but independent) distributions with μ and σ such that the probability of B finishing after A is 55%.
The probability of A winning is the probability that both B and C finish later, i.e. 0.55² ≈ 0.3.
The probability that at least one of B and C finishes before A is 0.7.
By the symmetry of the situation, P(B) = P(C) = 0.35.
So A is more likely to beat B than B is to beat A, likewise with A and C. But B and C are each more likely to finish first of the 3 than A.

I 'm not sure of what you say.
Doing this with Monte Carlo random numbers (Box-Muller) does n't seem to help.
With n = 2 and 100,000 samples it even finds errors, P(2) > P(1) and we know that for n=2, P(2) < P(1).

The proof for n = 2 exists somewhere but I don't have the proof that the order 1 > 2 is strictly valid only for n = 2. But if they integral says so then it is so unless some error is introduced by the Simpson rule approximation.

 

[cosmicminer]

I try

μ1 = 60, σ1 = 0.001
μ2 = 60.05, σ2 = 3

Integral says ok, P1 = 0.512884, P2 = 0.487116

Monte Carlo with 100,000 Box-Muller samples finds "error":

P1 = 0.48982, P2 = 0.51018

I add a μ3 = 60.05, σ3 = 3, so it's 3-way contest.
Integral finds P1 = 0.2598426, P2 = 0.3700787, P3 = 0.3700787
Monte Carlo with 100,000 Box-Muller samples again finds:
P1 = 0.27264, P2 = 0.35933, P3 = 0.36803

So it seems Monte Carlo finds it difficult even with 100,000 samples, while the integral says that the strict ordering is for n = 2 only.
27% to 36% looks like big difference to be caused by integration errors.

However when I increase the steps of integration from 200 to 1000 I find:

for n = 2, P(1)= 0.50519, P(2) = 0.4948101
for n = 3, P(1) = 0.2559455, P(2) = 0.3720273, P(3) = 0.3720273

So 200 to 1000 affects the second decimal digit.