Juntao
- 45
- 0
I've added a picture that's part of the problem.
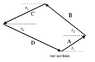
A sailboat race course consists of four legs defined by the displacement vectors A, B, C and D shown above.
The values of the angles are È1 = 420, È2 = 410, and È3 = 270.
The magnitudes of the first three vectors are A = 3.7 km, B = 5.3 km and C = 4.8 km. The finish line of the course coincides with the starting line.
The coordinate system for this problem has positive x to the right, positive y as up and counter-clockwise to be a positive angle.
------------------------------------------------------------------
Now first thing I should do is break up each vector into its components, and then add up all the x and y components to get vector D.
This is what I've tried.
Vector a
x-component = 3.7*cos 42=2.75km
y-component = 3.7*cos42= 2.48km
vector b
x component = 5.3*cos 41=4.00km
y component = 5.3*sin41= 3.48km
vector c
x component = 4.8*cos 27=4.27km
y component= 4.8*sin27= 2.18km
-------------------------------------------------------------------
vctor d
x component = 11.02km
y component = 8.14km
So for vector d, just add up the first 3 components in their respective columns. However, when I calculate D's distance => sqrt(11.02^2+8.14^2), I get the incorrect answer of 13.70km.
So of course, if this answer is wrong, then most likely I figured out one of the components wrong, but I don't know which ones. Please help.
A sailboat race course consists of four legs defined by the displacement vectors A, B, C and D shown above.
The values of the angles are È1 = 420, È2 = 410, and È3 = 270.
The magnitudes of the first three vectors are A = 3.7 km, B = 5.3 km and C = 4.8 km. The finish line of the course coincides with the starting line.
The coordinate system for this problem has positive x to the right, positive y as up and counter-clockwise to be a positive angle.
------------------------------------------------------------------
Now first thing I should do is break up each vector into its components, and then add up all the x and y components to get vector D.
This is what I've tried.
Vector a
x-component = 3.7*cos 42=2.75km
y-component = 3.7*cos42= 2.48km
vector b
x component = 5.3*cos 41=4.00km
y component = 5.3*sin41= 3.48km
vector c
x component = 4.8*cos 27=4.27km
y component= 4.8*sin27= 2.18km
-------------------------------------------------------------------
vctor d
x component = 11.02km
y component = 8.14km
So for vector d, just add up the first 3 components in their respective columns. However, when I calculate D's distance => sqrt(11.02^2+8.14^2), I get the incorrect answer of 13.70km.
So of course, if this answer is wrong, then most likely I figured out one of the components wrong, but I don't know which ones. Please help.
Attachments
Last edited: