Satellite Orbital Transfers: How to Calculate Work Done by Rocket Motors

[pureouchies4717]

hi everyone. I am having a little bit of trouble on this and was wondering if someone can help. i don't understand how to answer parts c and f

this is the picture:

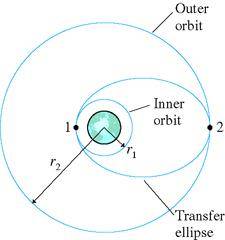
a)Consider a 1000 kg communication satellite that needs to be boosted from an orbit 300 km above the Earth to a geosynchronous orbit 35,900 km above the earth. Find the velocity v_1 on the lower circular orbit.
answer: 7730m/s
b) Find the velocity v_1' at the low point on the elliptical orbit that spans the two circular orbits.
Answer: 1.02 x 10^4 m/s
c) How much work must the rocket motor do to transfer the satellite from the circular orbit to the elliptical orbit?
Answer: ?
d) Now find the velocity v_2' at the top of the elliptical orbit
Answer: 1600 m/s
e) Now find the velocity v_2 of the upper circular orbit.
Answer: 3070 m/s
f) How much work must the rocket motor do to transfer the satellite from the elliptical orbit to the upper circular orbit?
Answer: ?
g) Compute the total work done.
Answer: 2.51 x 10^10 J

i know that c and f equal 2.51 x 10^10 J when added up. However, i don't understand how to get the work done to get this ship to the elliptical orbit and then to the outer orbit

please help. thanks,
nick

 

[pureouchies4717]

this is what my book says:

The work is the total work done in both burns. it takes a more extended analysis to see how the work has to be divided between the burns.

...real helpful haha

basically, i just know how to find the work done on geosynchronous orbits

 

[andrevdh]

Since the satellite is experiencing only a conservative force its total mechanical energy in each of the orbits will be constant. But to transfer it from one orbit to the other the rocket needs to do work to alter its total mechanical energy so that it will go into the new orbit (with a different total mechanical energy $E$). Since the orbital transfers is happening at the points in the elliptical orbit where its motion is purely tangential only the kinetic energy of the satellite need to be changed by the rocket.

 

[nrqed]

this is what my book says:



...real helpful haha

basically, i just know how to find the work done on geosynchronous orbits

Calculate the total energy in the first cicrular orbit. Then calculate the total energy in the transfer (elliptical) orbit (If I recall correctly, it's ${- G m M \over 2 a }$ where a is the semimajor axis). The difference will be the work done by the rockets (the transfer orbit will obviously have a larger energy)

At the arrival, calculate the difference between the total energy of the transfer orbit and the larger circular orbit (the latter will have a larger energy). That's the work done by the rockets there.

Patrick