Schrodinger's Equation in terms of vacuum permittivity?

[currently]

Summary:: How can Schrödinger's Equation be written relative to vacuum permittivity

I am wondering why a particular problem uses this equation:

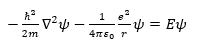
It is stated to be Schrödinger's equation. Where does the potential come in, as well as the e^2/r ?
An explanation would be greatly appreciated. Thanks.

 

[PeterDonis]

a particular problem

What problem? Please give a reference.

 

[currently]

What problem? Please give a reference.

Here's the problem. the equation was stated in class to be Schrödinger's Equation.
Last problem should say: n, l, and m are arbitrary constants.

 

[PeterDonis]

the equation was stated in class to be Schrödinger's Equation

It is. More precisely, it's the time-independent Schrödinger Equation, i.e., it's the eigenvalue equation that stationary states have to satisfy.

Where does the potential come in, as well as the e^2/r ?

The $e^2 / r$ term is the potential; it's the Coulomb potential due to the nucleus, in SI units.

 

[PeterDonis]

Moderator's note: Moved thread to homework forum.

 

[currently]

It is. More precisely, it's the time-independent Schrödinger Equation, i.e., it's the eigenvalue equation that stationary states have to satisfy.
The $e^2 / r$ term is the potential; it's the Coulomb potential due to the nucleus, in SI units.

Ok, thank you. I wanted to make sure it was the correct equation.