tomw87
- 2
- 0
Hi all, first post here but I've long browsed these forums for answers in the past.
I couldn't find an answer to my question through searching but I appologise in advance if it has been asked before.
I want to find an expression which relates second moment of area to the angle that the shape in question has rotated through.
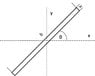
If you picture a rectangle with (for example) sides a = 1 and b = 10, with the neutral axis running through the centre of the rectangle, parallel to the long sides.
At 0 and 90 degrees of rotation about the centre of the rectangle you can use bd^3/12 to work out the second moment of area. However between these two I know you need to integrate, but I can't quite picture how this would work.
I know that I can use:
(int) y^2 da
(int)(int) y^2 dydx
The problem is how to define the limits and then to solve the integration as the limits are both functions of theta (angle that the rectangle makes with the x - axis) rather than just x & y as in a static problem.
If the width of the rectangle (a) was zero then the two limits would be on top of each other (obviously the area would then be zero).
However, in that case trig would suggest that x = cos(theta)*b and y = sin(theta)*b,
As the rectangle has a width there needs to be two pairs of functions with terms which determine their y-intersect in terms of the rectangles rotation.
I've attached an image showing the problem to make it a little clearer. This problem isn't urgent but I will keep thinking about it until I've solved it so any help would be appreciated!
Thanks in advance, Tom
I couldn't find an answer to my question through searching but I appologise in advance if it has been asked before.
Homework Statement
I want to find an expression which relates second moment of area to the angle that the shape in question has rotated through.
If you picture a rectangle with (for example) sides a = 1 and b = 10, with the neutral axis running through the centre of the rectangle, parallel to the long sides.
At 0 and 90 degrees of rotation about the centre of the rectangle you can use bd^3/12 to work out the second moment of area. However between these two I know you need to integrate, but I can't quite picture how this would work.
Homework Equations
The Attempt at a Solution
I know that I can use:
(int) y^2 da
(int)(int) y^2 dydx
The problem is how to define the limits and then to solve the integration as the limits are both functions of theta (angle that the rectangle makes with the x - axis) rather than just x & y as in a static problem.
If the width of the rectangle (a) was zero then the two limits would be on top of each other (obviously the area would then be zero).
However, in that case trig would suggest that x = cos(theta)*b and y = sin(theta)*b,
As the rectangle has a width there needs to be two pairs of functions with terms which determine their y-intersect in terms of the rectangles rotation.
I've attached an image showing the problem to make it a little clearer. This problem isn't urgent but I will keep thinking about it until I've solved it so any help would be appreciated!
Thanks in advance, Tom