Taylor_1989
- 400
- 14
Homework Statement
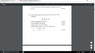
Hy guys I am have a problem with the last part of this question. part d), ii) I get the general formal which I have displayed below, but what I done understand is if I take the limits as show in ii) I get ##0=\
\infty## which obviously I am doing something wrong. Have I misinterpreted what they are say as y tends to 0 as x tends. Could anyone give me some advice it would be much appreciated, thanks in advance.
Homework Equations
The Attempt at a Solution
##y=c_1e^{2x}+c_2e^{-3x}-e^{-x}##