- #1
henrybrent
- 57
- 0
%PLOTTING TIME DEPENDENT MOTION OF A STANDING WAVE
%Define Parameters
a_n = 1;
k = 5;
w_n = 5;
x = 0:0.05:4;
t = 1:0.05:20;
for j=1:length(t)
for i=1:length(x)
u(i) = a_n*sin(k.* x(i)).* cos(w_n.*t(j)); %Formula for displacement
end
pause (0.1)
plot(u)
axis([1,65,-1.5,1.5])
grid on
end
Above is the code for a standing wave along a string. I need to create a few more of these, to end up with a series of standing waves which I can then calculate the sum of, which gives me the net displacement of the wave. I then need to plot this net displacement, which will result in a traveling wave.
Equation 1 on the formula sheet attached is the equation that governs the source that generates the series of standing waves. Tau is a 'tuning parameter'. I can just assign it a value. It determines the angular frequency. Imagine plucking a guitar. That is the source. We pluck the string of a guitar at a certain distance along the string. That distance is denoted as X_s (X subscript s). That can just be a value.
Equation 2 is the displacement for the nth standing wave (harmonic) where L is the length of the string, x is displacement and w_n (omega subscript n) is the angular frequency n is the harmonic number. I need to incorporate this somehow into the loop I have used to generate the wave in my code, in order to plot, let's say, the first 5 harmonics as subplots.
Equation 3 is then used to sum all of these harmonics together, to generate a final plot.
Any ideas on how to do this using the code and formula I have written
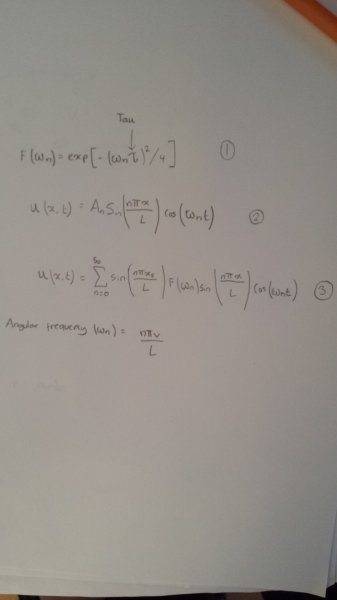
%Define Parameters
a_n = 1;
k = 5;
w_n = 5;
x = 0:0.05:4;
t = 1:0.05:20;
for j=1:length(t)
for i=1:length(x)
u(i) = a_n*sin(k.* x(i)).* cos(w_n.*t(j)); %Formula for displacement
end
pause (0.1)
plot(u)
axis([1,65,-1.5,1.5])
grid on
end
Above is the code for a standing wave along a string. I need to create a few more of these, to end up with a series of standing waves which I can then calculate the sum of, which gives me the net displacement of the wave. I then need to plot this net displacement, which will result in a traveling wave.
Equation 1 on the formula sheet attached is the equation that governs the source that generates the series of standing waves. Tau is a 'tuning parameter'. I can just assign it a value. It determines the angular frequency. Imagine plucking a guitar. That is the source. We pluck the string of a guitar at a certain distance along the string. That distance is denoted as X_s (X subscript s). That can just be a value.
Equation 2 is the displacement for the nth standing wave (harmonic) where L is the length of the string, x is displacement and w_n (omega subscript n) is the angular frequency n is the harmonic number. I need to incorporate this somehow into the loop I have used to generate the wave in my code, in order to plot, let's say, the first 5 harmonics as subplots.
Equation 3 is then used to sum all of these harmonics together, to generate a final plot.
Any ideas on how to do this using the code and formula I have written