bakin
- 55
- 0
I just have a quick question. I'm supposed to find the work required to pump gas out of a cone, but am having trouble finding the radius of the cone.
The cone measures 10 feet in height. I broke it up and set it up using similar triangles, and this is what I got:
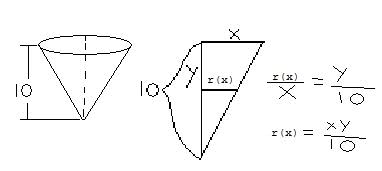
It doesn't seem right though. And, if it is right, where do I go from there? Any help is appreciated :)
The cone measures 10 feet in height. I broke it up and set it up using similar triangles, and this is what I got:
It doesn't seem right though. And, if it is right, where do I go from there? Any help is appreciated :)