- #1
Dell
- 590
- 0
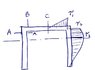
in a question i am asked to calculate the shearing force in a nail holding a cross section together, the cross section is showed in my diagram.
my problem was that after calcultions i found that the centroid of the entire cross section was the same as the centroid of the secondary piece(the block) being nailed to the channel cross section, meaning when i calculate the shear flow (looking only at the block) i get zero, because Q=0,(Q=y*A and y=0), q=VQ/I=0
i checked this by calculating the shear flow in 2 other ways and comparing and i really found that the shear flow at the point of the nail is zero, can this be?? is this a trick question?
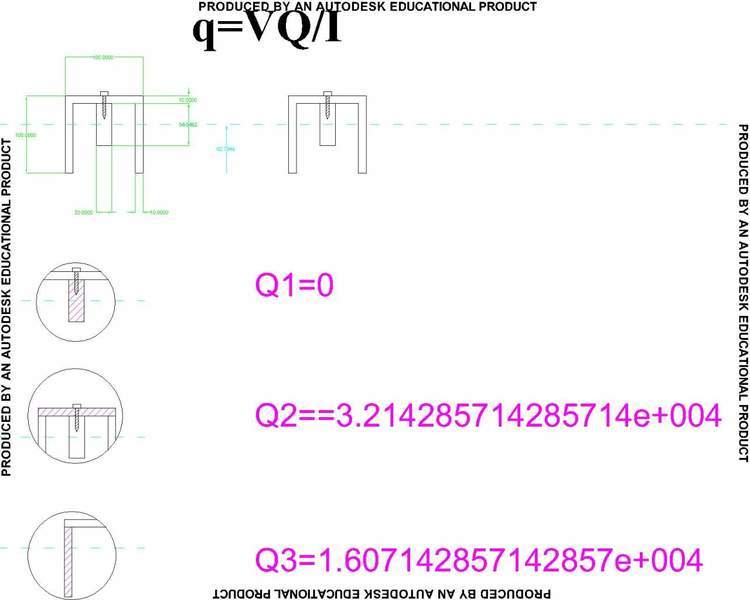
my problem was that after calcultions i found that the centroid of the entire cross section was the same as the centroid of the secondary piece(the block) being nailed to the channel cross section, meaning when i calculate the shear flow (looking only at the block) i get zero, because Q=0,(Q=y*A and y=0), q=VQ/I=0
i checked this by calculating the shear flow in 2 other ways and comparing and i really found that the shear flow at the point of the nail is zero, can this be?? is this a trick question?