Myr73
- 120
- 0
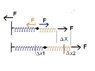
A mass m slides on a frictionless horizontal surface, connected to two springs, as shown below. If the force have constants K1 and K2 , show that the simple harmonic sliding motion has period.
T= 2 Pie (Square Root X m { K1+K2/K1K2})
So far I have →From equation T= 2Pie{SquareRoot(m/k)
If these two equations are the same, k must equal { K1+K2/K1K2}.
It may just be the calculus that I am not understanding but I don't know how to show that
k= { K1+K2/K1K2}. How would I begin this?
T= 2 Pie (Square Root X m { K1+K2/K1K2})
So far I have →From equation T= 2Pie{SquareRoot(m/k)
If these two equations are the same, k must equal { K1+K2/K1K2}.
It may just be the calculus that I am not understanding but I don't know how to show that
k= { K1+K2/K1K2}. How would I begin this?