Maddie1609
- 81
- 11
Homework Statement
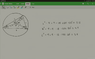
The corners A, B and C of a triangle lies on a circle with radius 3. We say the triangle is inscribed in the circle. ∠A is 40° and ∠B is 80°.
Find the length of the sides AB, BC and AC.
Homework Equations
The Attempt at a Solution
I found out the arc AB is 2π, arc BC is 4π/3 and arc AC is 8π/3. Don't know if it's relevant, but I did it nonetheless. The book says nothing about finding the arc or finding the lengths, the question came out of nowhere. It's a shitty book to say the least. Don' really know where to go from here. Is there a constant ratio between length of sides of a central angle and something else?