Timburton91
- 3
- 0
- Homework Statement
- Damped Simple Harmonic Motion
- Relevant Equations
- x(t)=e^-kt cos(2πft)
Hi guys sorry if this is the wrong thread,
I have a damped simple harmonic motion pictured below, i have to find the inerval t=0 and t=1 for which the amplitude of x(t) is considered to be zero.
The behaviour of the graph below can be described as e^-kt cos(2πft)
k=0.7s^-1 and f= 3Hz
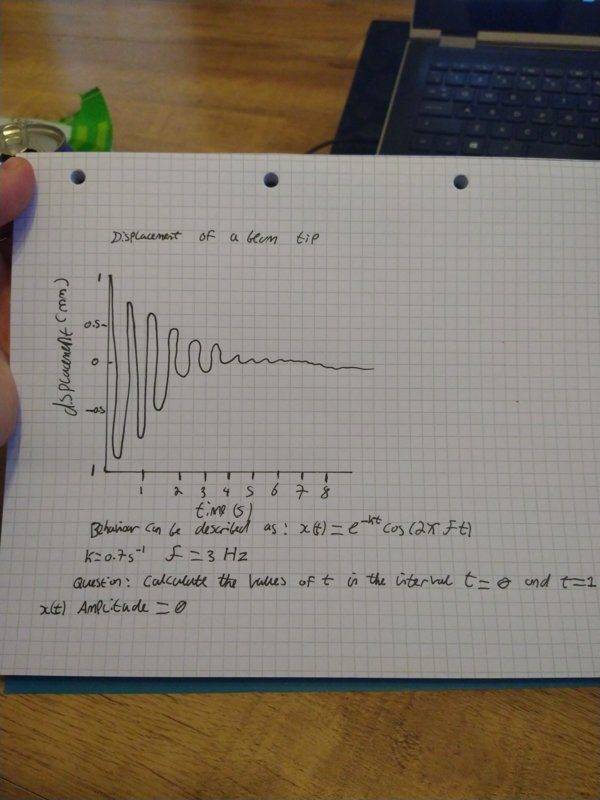
I have a damped simple harmonic motion pictured below, i have to find the inerval t=0 and t=1 for which the amplitude of x(t) is considered to be zero.
The behaviour of the graph below can be described as e^-kt cos(2πft)
k=0.7s^-1 and f= 3Hz
Last edited: