Simple parallel circuit question

[jgv115]

Ok so my maths department decided to give us a question about electrical circuits with no information on how they work. Considering that more than half of the students are only starting their physics study this year (including me) it seems a bit odd... I just need a bit of clarification on a few things.

Diagram here:

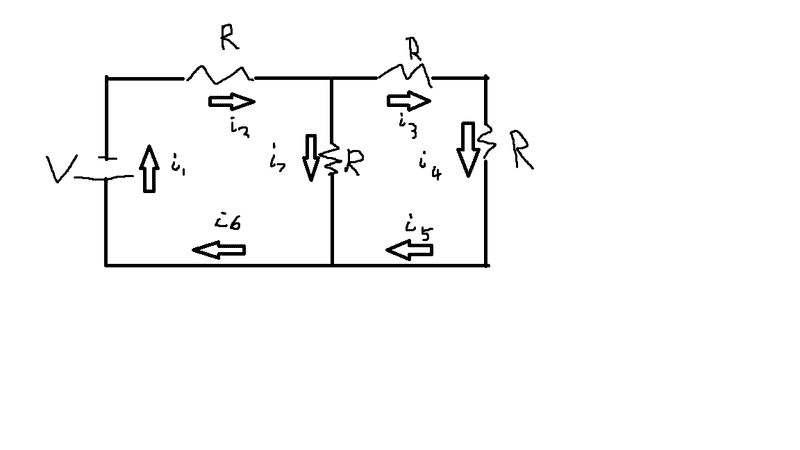
I understand that Kirchoff's Law says that the total change in electrical potential around a closed loop is zero.
So that means we have... V = i_{2}R + i_{7}R and also V= i_{3}R + i_{4}R. Is this correct so far?

Another law I found was that the sum of all currents at any node in the circuit is zero..

So we have... i_{2} -i_{3} - i_{7} = 0 and i_{5} + i_{7} - i_{6} = 0

If this is all correct, then I have 4 equations... I need a total of 7 to solve for the values of the currents in terms of V and R.

Unfortunately, that is as far as my knowledge takes me... Could someone point me in some direction as to how I could find the other equations.

Is by any change i_{3} = i_{4} = i_{5} and i_{1} + i_{2} + i_{6}

Thanks in advanced

 

[NascentOxygen]

Hi jgv115! http://img96.imageshack.us/img96/5725/red5e5etimes5e5e45e5e25.gif

Current doesn't evaporate or get used up, so i3 = i4 = i5
and i1 = i2 = i6
and i7 + i5 = i6

If your arrows indicate current direction, then they should all be reversed because current goes from the large (+) terminal then around the circuit and back into the battery's stubby terminal. (As your diagram stands, the arrows are correct for electron flow. Conventional current is said to flow in the opposite direction―an historical anomaly.)

 

[jgv115]

Hi, NascentOxygen

Thanks for the simple explanation (which is all I needed for this maths question).

Could you perhaps confirm whether or not V= i_{3}R + i_{4}R

I'm just a bit worried that because the current gets split at the top node that this somehow isn't correct.

Thank you

 

[pbuk]

Could you perhaps confirm whether or not V= i_{3}R + i_{4}R

No, you have missed a resistor out of that closed loop.

 

[jgv115]

Hmm... does that mean I'm missing the resistor above i_{2}?

That makes it V= i_{3}R + i_{4}R + i_{2}R. Is that right?

 

[pbuk]

Yes that's right! Does it help if you simplify the whole thing e.g. by setting $j = i_7$ and $k = i_3 = i_4 = i_5$ ? You then only have two variables so only need two equations, and you have two closed loops over which you can apply Kirchoff's Law...