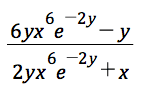Prove $$\int\limits_0^{\sqrt2/4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx = \frac{\pi^2}{8}.$$
Let $$I = \int\limits_0^{\sqrt 2 / 4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx. \tag{1}$$
The representation integral of ##\arcsin## is $$\arcsin u = \int\limits_{0}^{1} \frac{\mathrm dt}{\sqrt{1-t^2}}, \qquad 0 \leqslant u \leqslant 1.$$
Plugging identity above into ##(1)## with ##u...