FirePhoenix
- 2
- 0
Hallo,
i'm trying to implement a comsol simulation of a impedance spectroscopy experiment.
But unfortunatly I'm an absolut beginner in Comsol and i have many problems with this work.
First of all i want to say that I'm using the AC/DC module, more precisely the transient analysis.
At the moment I'm using a simple 2D geometry to try out all equations and boundary conditions.
Now to the first problem:
I tried to simulate only a double layer capacitance between an electrode and a drop of water. The double layer thickness is very small compared to the dimensions of the electrodes, so I didn't want to draw it, but use a distributed impedance for the boundary condition between the electrode and the drop of water.
The other boundary conditions are:
Potential V= sin(10*t) on the left side of the electrode.
Potential V= -sin(10*t) on the right side of the drop of water.
All other boundaries are electrical insulated.
But it wasn't sucessfuly, I always receive the whole potencial difference over the drop of water and not over the distributed impedance.
The second problem is that I have no idea how to bring the warburg impedance equation into the boundary conditions.
The equation is something like Z= sigma/sqrt(w)*(1-j), but where do I place that and how can i express w?
Finaly remains the question, if it is possible to make the simulations automatic over a defined range of frequencies and to calculate a complex impedance out of the result.
Attachments:
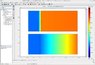
Comsol1: result, up a simulation with a drawed double layer, down the distributed impedance.
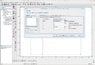
Comsol2: the boundary condition for the distributed impedance
Comsol3: the boundary condition of the electrode
thanke you for your help
and sorry for my bad english
cu FirePhoenix
i'm trying to implement a comsol simulation of a impedance spectroscopy experiment.
But unfortunatly I'm an absolut beginner in Comsol and i have many problems with this work.
First of all i want to say that I'm using the AC/DC module, more precisely the transient analysis.
At the moment I'm using a simple 2D geometry to try out all equations and boundary conditions.
Now to the first problem:
I tried to simulate only a double layer capacitance between an electrode and a drop of water. The double layer thickness is very small compared to the dimensions of the electrodes, so I didn't want to draw it, but use a distributed impedance for the boundary condition between the electrode and the drop of water.
The other boundary conditions are:
Potential V= sin(10*t) on the left side of the electrode.
Potential V= -sin(10*t) on the right side of the drop of water.
All other boundaries are electrical insulated.
But it wasn't sucessfuly, I always receive the whole potencial difference over the drop of water and not over the distributed impedance.
The second problem is that I have no idea how to bring the warburg impedance equation into the boundary conditions.
The equation is something like Z= sigma/sqrt(w)*(1-j), but where do I place that and how can i express w?
Finaly remains the question, if it is possible to make the simulations automatic over a defined range of frequencies and to calculate a complex impedance out of the result.
Attachments:
Comsol1: result, up a simulation with a drawed double layer, down the distributed impedance.
Comsol2: the boundary condition for the distributed impedance
Comsol3: the boundary condition of the electrode
thanke you for your help
and sorry for my bad english
cu FirePhoenix