I Simultaneity and the Twin Paradox

[Janus]

@PeterDonis: I like to work things out fully for myself, which takes time. I understand things better when I can crank through all the logic on my own.

I thought I had found an error in my work. This just told me my conclusions were wrong, but it didn't provide a solid understanding of why. Thus, I revisited the thread and re-read a number of your posts.

I realized I still didn't understand how BN could read A's clock as 1.8. Tracing through your comments, I think the problem starts here:
If I take this approach, I arrive at a logical contradiction. So I clearly still don't understand.

Let's look at things from A's frame only. Let's remove the infinite line of closely spaced B's and replace it with a line of B's that are spaced evenly 4 LY apart as measured by A. Traveling at 0.8c, A will expect to see a B pass by every 5 years. The math seems simple and unavoidable. Each time a B passes by and sees A, it should see that A's time is a multiple of 5 (if the first conjunction occurred at 0). I can't picture any other scenario that makes sense. We're are looking at things from A's view, but the event (and A's clock reading) is in all frames.

I'm not looking at things from B's frame at all. It shouldn't matter. A's viewpoint provides all the information I need. We don't care about B's clock anywhere, just about what A's clock says at conjunctions.

You tell me that the first trailing B (what you call BN) will see A's clock as reading 1.8 years at conjunction. I can't see how. Help!

This is really the heart of my objection. What follows is just details.

--------------------------------------------------------------------------------

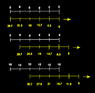
Let me draw the clocks based on your statement about clock synchronization. I am going to add a line of A's, also spaced 4 LY apart as measured by A.

A . . . . A . . . . A . . . . A . . . . A
B . . . . B . . . . B . . . . B . . . . B
^-7.2 . .-5.4 . . .-3.6 . . .-1.8 . . . 0
^-5.4 . . .-3.6 . . .-1.8 . . . 0
-3.6 . . .-1.8 . . . 0
^-1.8 . . . 0
^0
The caret points to the corresponding B's view of each of A's clocks at B's time 0. The time listed under each A, is the time as perceived by the B with the caret. As I imagine movement in typical Western left-to-right fashion, the rightmost A is the one that we've been concerned with. The rightmost B is the "lead B" or B1. All times are for when the lead B is at time 0, so all B's perceive the lead A to have time 0. This is my interpretation of your statement.

The other times are what I think they would be so that B would perceive A's clocks advancing by 1.8 years as one B went to the next. If we advance this diagram by 3 years (B's time) or 5 years (A's time), the trailing B would say that the lead A's clock reads 1.8, which I believe to be impossible.

Here's the way I think things should like so that B sees a multiple of 5 at each conjunction. B also sees A's clocks advancing by 1.8 years during the trip:

A . . . . A . . . . A . . . . A . . . . A
B . . . . B . . . . B . . . . B . . . . B
^0 . . . 3.2 . . . 7.4 . . . 9.6 . . . 12.8
^0 . . . 3.2 . . . 7.4 . . . 9.6
^0 . . . 3.2 . . . 7.4
^0 . . . 3.2
^0

In this example, the last B would reach A (the lead A) in 4 * 3 = 12 B years (4 * 1.8 = 7.2 years A years from B's view) and A's clock would read 7.2 + 12.8 = 20.

In my diagram, when B's clocks are at time 0, each adjacent A's clock also reads 0. But the lead A's clock reads 0 only for the lead B.

I have no idea if this diagram is a representation of how things work. All I can say is that it satisfies these two constraints: A's clocks are a multiple of 5 at conjunctions and B's perceive A's clock as running at 0.6x (assuming I did the math right, always a concern).

Events according to A's clocks (white)

Events according to B's clocks (yellow)

 

[Freixas]

Yes, but my point is that those in motion relative to you may not necessarily agree that you've made the correction for light travel time correctly, and that's the reason why you think they're simultaneous. All will agree, though, that each frame of the movie was made before it was viewed.

Not a problem. It's OK if others have different views. You make the correction in your frame and see what results.

And yes, the video is always generated after the fact.

 

[Freixas]

Events according to A's clocks (white)
View attachment 229015

Events according to B's clocks (yellow)

View attachment 229016

Thanks!

 

[PeterDonis]

the B adjacent to A when A sends the "2.4 year" frame should have a clock reading of 3 years, no?

No. We have already established that the B that has a clock reading of 3 years when it passes A (which is BN) sees A's clock reading 1.8 years. So that will be the A clock reading in the video frame emitted by A at that event.

That makes me wonder what I did specify.

I think a key issue you have not realized is that there are three different things you could specify, and they are not independent:

(1) You could specify the spacing of the B clocks in the A frame;

(2) You could specify the reading on the B clock "adjacent" to B1 when it passes clock A;

(3) You could specify the reading that the B clock "adjacent" to B1 sees on clock A when it passes it.

Once you have specified anyone of these three things, the other two are fixed. At different points in this thread, you have specified all three of these: 4 LY for (1), 3 years for (2), and 5 years for (3). It turns out that 4 LY for (1) and 5 years for (3) specify the same scenario (the same set of values for all three things); but 3 years for (2) does not. So you have specified at least two different and mutually inconsistent scenarios in this thread, and have not kept track of which one you are talking about, so you are mixing numbers from the two, which of course is going to confuse you.

Just to quickly summarize the two sets of values: the "clock BN" scenario specifies 3 years for (2); and the other two values fixed by this specification are 1.44 LY for (1) and 1.8 years for (3).

The "clock BA" scenario specifies 4 LY for (1); and the other two values fixed by this specification are 8 1/3 years for (2) and 5 years for (3). (At other points you have specified 5 years for (3), which gives the same scenario.)

Note also the relationships between the three numbers. The number for (1) will be $v$ times the number for (3); and the number for (2) will be $\gamma$ times the number for (3). That is the simplest way to calculate the other two numbers from anyone of them.

It should have said 0 to 2.4 years over a 3 year period.

No, 0 to 1.8 years over a 3 year period. See above.

I think the correct statement is: BN's clock reads 3 years when it reaches A, so the video
frame at 3 years should show 2.4.

No, 1.8. See above.

BN is not one of the ships that shows up in A's skies every 5 years, just the ship that is alongside A when its clock hits 3.

Yes.

Where was BN when it's clock read 0?

Well, if clock B1 was at $x = 0$ when it reads 0, and at $x = 4$ when it reads 3 years; then if clock BN is at $x = 0$ when it reads 3 years, it should be at $x = -4$ when it reads 0, no? (But note that this will not be at the event $(x, t) = (4, 0)$. Can you figure out what--negative--value of $t$, in the A frame, clock BN will read zero at? You should be able to use similar reasoning to what I just used to figure out the $x$ coordinate of that event--by comparison with B1--using the fact that BN's clock reads 3 years at $t = 1.8$.)

I'm sure I just added some new errors.

Yes. But you're making progress. See above.

 

[Freixas]

Yes. But you're making progress. See above.

Thanks. I really need to sit down and work this through. But thanks for at least blocking some wrong paths.

 

[Freixas]

@PeterDonis: I set up a spreadsheet with the Lorentz transforms, which I should have done some time back. The problem with using the Lorentz transforms is in setting up the problem properly so you understand what you're asking and what the results mean. It still might have been more productive to work through the transform earlier on. I wouldn't have set things up right, but you could have corrected the setup. Oh, well, better late than never.

So a ship in B's frame that passes A when its clock reads 3 years, sees a time of 1.8. So I have to conclude that this is not equivalent to having B correct for light delay. Or is it? I need to verify the light delay calculation.

B (or B1 if you prefer) receives video frame 1 at M. It is now 2.4 LY from A, but (as you pointed out earlier), after A sent the video, A continued to move further away (B's view) so where it is now is not where it was when it sent the frame.

So my correction formula is:

• Video frame is received at time t_rec
• Video frame was sent at t_sent
• Sending object is now at distance d
• Sending object is moving away at v
• t_sent = t_rec - (d / (1 + v))

This is a formula I derived (which is why it needs checking!).

• The frame gets sent at t_sent
• For every unit of distance the light travels, the object recedes at v (where v is expressed as a fraction of c).
• The total distance d is equal to the distance from where the frame was sent plus the distance the object receded
• So d = d_sent * c + d_sent * v
• d = d_sent * (c + v) = d_sent * (1 + v)
• Solving for d_sent we get: d_sent = d / (1 + v)
• Because distances are in LY, d_sent tells us how long it took for the light to reach us
• We subtract d_sent from the current time to get the time the video was sent
• t_sent = t_rec - d_sent = t_rec - (d / (1 + v))

I use this formula in a spreadsheet where it seems to give reasonable answers. I had it just calculating frames 1, 2, 3, 4, etc. For B, frame 1 gets placed at 1 2/3 on the mapped video. Frame 5 gets placed at 8 1/3 on the mapped video (long after B passes M, so we don't use anything after 1).

OK, so where does frame 1.8 fall? I added a new row for it in the spreadsheet and it says 3. Huh? Where did I come up with 2.4 mapping to 3?

After reams and reams of messages and confusion (on my part), I finally come to the stunning realization that 0.6 * 3 = 1.8. It's 0.8 * 3 that equals 2.4, which is the number for how long it takes B to travel 3 LY at 0.8c. I did say somewhere and long ago, that I had a tendency to take 2 + 2 and get 22, so here's a multiplication table error that got its grip on me and wouldn't let go. Up until now, the 1.8 answer seemed weird; the weirdness just disappeared. I was using the wrong time dilation factor.

Bottom line: the line of trailing ships seems equivalent to calculating the light delay (if one can handle simple multiplication). Peter, I just hope you get a laugh out of this (as opposed to crying over all the time spent on posts trying to straighten me out).

 

[Herman Trivilino]

Not a problem. It's OK if others have different views. You make the correction in your frame and see what results.

My point is that when a person allows for light travel time he must assume a simultaneity convention. You are claiming that when you do you don't assume a simultaneity convention.

 

[PeterDonis]

t_sent = t_rec - (d / (1 + v))

Yes.

so where does frame 1.8 fall? I added a new row for it in the spreadsheet and it says 3.

Yes. Which means that, in the B frame, A's clock reads 1.8 years at B frame time 3 years.

the line of trailing ships seems equivalent to calculating the light delay

Yes. Or, to put it another way, the line of B ships is a physical realization of the "B frame". You have them all carrying clocks synchronized to B frame time; you could also have them carrying distance markers calibrated to B frame distance--so, for example, clock B1 would carry distance marker "0" and clock BN (the one that reads 3 years when it passes A) would carry distance marker "minus 2.4". Then you could read off the B frame position of A as well as the B frame time of A from the B ship that was passing A at any given point. And similarly for any other A ship, such as M--whichever B ship is passing M at any given point gives the B frame time and position of M at that point.

In fact, you could also think of the A ships as physically realizing the A frame in the same way. All of the ships have clocks synchronized to A frame time. Ship A would carry A frame distance marker "0" and ship M would carry A frame distance marker "4". Then the B ships could read off A frame time and position from the A ship they were passing at any given point.

 

[Freixas]

My point is that when a person allows for light travel time he must assume a simultaneity convention. You are claiming that when you do you don't assume a simultaneity convention.

It's possible I claimed that since this is a long thread and I've said a lot of stuff.

What I meant was that the simultaneity convention is for the observer who records the raw, uncorrected video. Anyone can later construct the mapped video, given some information about the setup and the raw video with embedded time codes (essentially, the local time during recording). See the long discussion above about an infinite line of B ships, all with synchronized clocks. The simultaneity convention assumption seems pretty explicit.

But I don't care about where the video is viewed which I think was what you were claiming. This is a completely different thing and I is completely irrelevant.

 

[Herman Trivilino]

It's possible I claimed that since this is a long thread and I've said a lot of stuff.

You did it in Post #92.

But I don't care about where the video is viewed which I think was what you were claiming.

No. What I was claiming was that when you allow for light travel time you adopt a simultaneity convention.

 

[PeterDonis]

the simultaneity convention is for the observer who records the raw, uncorrected video

Actually, that's not necessary, if the observer is truly recording just "raw" video. That is, if all the observer records is what is in the video frame he receives, and what time by his clock he receives it, then everything is an invariant and doesn't depend on any choice of coordinates or any simultaneity convention. For example, if B1 records that he received a video frame from A at time 3 years by B1's clock, and that frame showed A's clock reading 1 year, meaning that A emitted that video frame when A's clock read 1 year, those numbers are invariants; they don't depend on any simultaneity convention. The simultaneity convention only comes into play if B1 wants to calculate at what time in his frame (as opposed to what time by A's clock--the time by A's clock is right there in the raw data) A sent that video frame.

 

[Freixas]

You did it in Post #92.

I did no such thing in post #92.

No. What I was claiming was that when you allow for light travel time you adopt a simultaneity convention.

I don't disagree. However, you said "When you adjust for light travel time you are assuming that a clock located there (where the movie was made) is synchronized with a clock located here (where the movie is viewed)."

Where the movie is viewed remains totally irrelevant. PeterDonis correctly identifies where the simultaneity convention comes into play--in the calculation performed when mapping the raw video to created the mapped video. This has nothing to do with where the movie is viewed. Nor does it have anything to do with where the calculation is made or by whom.

 

[Freixas]

Long ago I proposed a thought experiment about creating a light-delay-corrected video so as to "see" the twins paradox in play.

To review: In A's inertial rest frame. B and C move away and toward him, respectively, both at 0.8c. When A and B meet, they synchronize their clocks at 0. A begins transmitting a video of his clock to B. B records the video. B eventually reaches M, a location 4 LY from A in A's frame and at rest relative to A. Here, B encounters C and gives C the video recorded thus far. C synchronizes his clock to B's, which now reads 3 years. C continues recording video from A. When C arrives at A, he transfers the video to A, who will attempt to construct a new video, with each video frame corrected for light delay as per B's or C's frame.

I'm going to simplify this a bit. B will continue recording video until a frame get mapped to 3 years. He won't be able to do this until he is long past M. He will ship his video back to A by interstellar post. A will assemble the video so the first 3 years come from B's footage and the last 3 from C's. Keep in mind that the frames represent where B (or C) was when they believe A sent a frame, so the 3 year mark of the mapped video is when B and C met at M.

Some people may not realize that video contains timecodes. In this case, the timecodes begin at 0 when B's clock is 0, and continue tracking local time. Anyone looking at the video later will have both the content of the video and the local clock reading when video was received. And yes, I realize each individual frame will need to be corrected for the relative Doppler shift in order to be viewable. We consider a video frame to arrive at the moment the first pixel is received.

My (self-imposed) assignment was to do the calculations for this scenario. Setting up the problem and working through all the equations was a learning experience for me. The video generated may not mean a thing, but the exercise was interesting and worthwhile. The simplification I used is not needed. Knowing all the parameters of the setup and when C receives frames sent on B's leg of the trip, one could calculate where B was when that frame was sent. When I say "one could", I don't include myself.

The video would be equivalent to that produced by a single traveler making an instantaneous turn-around--the infamous twins paradox. Since that is not possible, I think one could create an equivalent video where acceleration is used to turn around at M. Again, "one could" is even farther from being me, and I believe the calculations become a lot more difficult.

I have attached a spreadsheet showing my calculations. The spreadsheet contains two sheets: one labeled "Setup", which should be self-explanatory and another labeled "Simulation", which needs some explaining. Let me add a screen shot:

The first column shows the frames sent. To simplify further, I just calculated frames at 1 year intervals, with the exception of frames at years 1.8 and 8.2.

I've created sections for A's view, B's view, and C's view. The numbers in black represent things related to when a frame as sent. The numbers in red represent things related to when the frame was received (OK, technically, the mapped column shouldn't be red). For B, we ignore everything after we get a frame that maps to B's year 3, so these have a gray background.

C's view is a little cluttered. Gray represents frames that map to a position earlier than 3 years. However, the blue-green row is a frame that C receives and that B didn't (not until after M). We could use a different mapping to allow this frame to fill in the rest of B's leg of the trip (but I haven't). The following lines have a pink crosshatch. These are frames that don't map either to B's 3 year trip from A to M or C's 3 -year trip from M to A. They are tossed away.

The final column shows the mapped video. At the 3-year mark, we see A's 1.8 year frame. At the 3-year mark, we also see A's 8.2 frame. You can pick one or the other or blend them. However, you always see A's clock running slower, at at 0.6 rate to the video timecodes.

Three frames are highlighted by a box around their row. Frame 1 was the frame received when B and C were at M. Frames 1.8 and 8.2 are the frames that were sent when B and C were at M (one from B's view and one from C's view, of course).

This may be a trivial exercise for an experienced physicist or mathematician. The last time I attended a math class was before 1976, so I'm a little rusty. Plus I appear to have some sort of arithmetic dyslexia . Using a spreadsheet keeps me honest.

 

[Mentz114]

@PeterDonis: I set up a spreadsheet with the Lorentz transforms, which I should have done some time back. The problem with using the Lorentz transforms is in setting up the problem properly so you understand what you're asking and what the results mean. It still might have been more productive to work through the transform earlier on. I wouldn't have set things up right, but you could have corrected the setup. Oh, well, better late than never.

So a ship in B's frame that passes A when its clock reads 3 years, sees a time of 1.8. So I have to conclude that this is not equivalent to having B correct for light delay. Or is it? I need to verify the light delay calculation.

B (or B1 if you prefer) receives video frame 1 at M. It is now 2.4 LY from A, but (as you pointed out earlier), after A sent the video, A continued to move further away (B's view) so where it is now is not where it was when it sent the frame.
[..]

You've put a great deal of work into this twins and simultaneity thing but it is much easier to do it diagramatically in a Minkowski chart.
Here is a chart showing 3 spaceships moving on the x (horizontal) axis at different x-velocities. The diagram has one (blue) worldline at rest in the diagram frame. When the red and green ships pass, red sets their clock to green's reading.

I also made an animation which is here (http://www.blatword.co.uk/space-time/twins-3.mpeg)

The white line is the 'line of simultaneity, or 'now' in the blue frame. It cuts the worldlines at different times on the green and red worldlines. The important thing is that the intersection points are out side of their mutual past-lightcones, and so are not causally connected. This makes the definition of a universal 'now' problematical.

 

[Freixas]

You've put a great deal of work into this twins and simultaneity thing but it is much easier to do it diagramatically in a Minkowski chart.

Thanks. I know this is a really long thread, but I started in Post #1 with a Minkowski diagram. The spreadsheet (and the light-delay-corrected video) may not be of any value to anyone but me, but I found it useful to go through the exercise.

 

[Mentz114]

Thanks. I know this is a really long thread, but I started in Post #1 with a Minkowski diagram. The spreadsheet (and the light-delay-corrected video) may not be of any value to anyone but me, but I found it useful to go through the exercise.

Nonetheless you showed no understanding of what the diagram means ( actually it's not a good article) . I hoped my approach could help.
In answer to your question - 'can the diagram be redrawn for the traveling twin' is obviously 'yes' ( Lorentz transformation ).
The three traveller approach removes all argument about inertialess acceleration etc.

 

[pervect]

I'd like to say a few words about why we use the synchronization conventions we do.

Suppose you're trying to find the flight speed of a plane. Assume wind speed is negligible for this thought experiment to make the calculations easier. First you set up a course of known length for the plane to fly. You let the plane get up to speed, then you note the time on the wall clock the plane passes the "start" marker. When it reaches the "end" marker, you note the time on the wall clock at the end marker, which is a different wall clock because it's in a different location than the one at the start marker.

To get the travel time, you subtract the time on the end clock from the time on the start clock, and call that the trip time. And you divide the length of the course by the trip time to get the plane's speed.

Now, imagine that you did this exercise with the clocks being corrected for the local timezone. You'd find that the plane flies much faster to the west than the east, arriving at almost the same time it took off it it's a jet plane.

Does this hurt anything? IT depends on what you're doing. It's defintely non-physical. I'd argue that the number isn't "really" speed, it's something you calculate that's not physical, and because it defies common conventions, it's misleading.

If the plane was even faster, things would be even worse. For instance if it wasn't a commercial jet, but a supersonic military plane, one might find that the plane arrived before it left, so the speed number one calculated was negative of what it "should" be.If one does not use the Einsteinian clock synchronization in a frame, the same thing basically happens as happened with the plane. The numbers that one calculates for speed based on techniques like the above will be misleading, and quantities like momentum and energy that one might caclulate from the speed with the usual high-school Newtonian sorts of formulas will be totally wrong. The issue with fast moving objects ariving before they left might also arise, depnding on how far off the clock synchorization was from the standard approach.The situation is not terribly different for the issue of relativistic clock syncrhonization. It's basically the same issues, just that the speeds are faster and the times are shorter. If one has ever traveled cross country from one timezone to another, the plane issue may well be one one has experienced.

It is possible to do physics correctly with such non-physical numbers, by , for instance, tensor techniques, but that takes some specialized knowledge and isn't particularly intuitive. I wouldn't in general recommend it, and espically not for somone struggling to learn physics. If one uses such numbers in the usual formula for physical quantites such as momentum or energy, the answers one gets will be wrong.

 

[PeterDonis]

In answer to your question - 'can the diagram be redrawn for the traveling twin' is obviously 'yes' ( Lorentz transformation ).

This is true if by "the traveling twin" you mean either the twin's outbound rest frame, or the twin's inbound rest frame. It is not true, however, if you mean a frame in which the twin is at rest for his entire trip (outbound and inbound); any such frame is not inertial and cannot be obtained from the stay-at-home twin's rest frame by a Lorentz transformation.

 

[PeterDonis]

At this point it looks like every relevant viewpoint has been expressed in this thread multiple times, and the discussion is getting long enough that thins are being repeated. Accordingly, the thread is closed.