Simultaneity and the Twin Paradox

[Freixas]

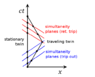
Here is a diagram from the Wikipedia. I'm sure you understand what this represents. Those who don't, can go to the Wikipedia page (https://en.wikipedia.org/wiki/Twin_paradox) and see all the details.

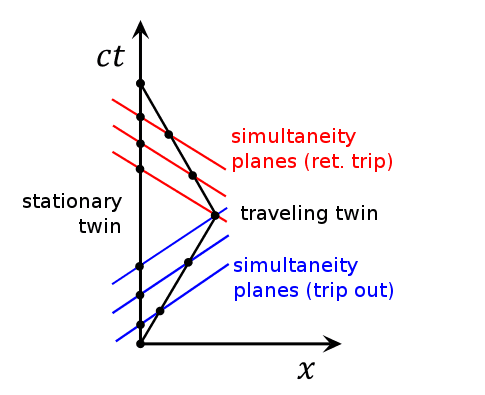
After my prior post, I have a better appreciation for simultaneity. Originally, when I looked at this diagram, I looked at it using the common meaning of "simultaneous". I thought it was telling me that where the red and blue lines cross the space time lines of the stationary and traveling twins, the twins exist in the same moment from both twin's perspectives.

My insight is that the correspondence is just for the traveling twin. The stationary twin will draw different lines. The word (on the chart itself!) "simultaneity" really tripped me up. I'll be honest; even when the diagrams included the stationary twin's idea of simultaneous, I didn't really understand what I was looking at. There's seeing and there is understanding.

I'm sure this is so ingrained with experienced physicists that they may not understand why throwing these diagrams at beginners doesn't make things crystal clear. I mean, you even tell the poor beginner what the lines means and he still doesn't get it. Diagrams like this that omit the other twin's simultaneity lines tend to support the wrong idea.

Yes, there is a question here. Two, actually.

The diagram above assumes the traveling twin can change directions instantaneously. I want to check my understanding. The stationary twin can look at a giant clock attached to the traveling twin. He records the clock and then corrects the recording for light delay. I believe he sees the traveling twin's clock running slow by the same factor on each leg of the trip.

The stationary twin also has a clock that the traveling twin can record. The traveling twin corrects his recording for light delay. He also sees his stationary twin's clock running slower and by the same amount on each leg. However, at turn-around, he sees his twin's clock jump forward in time. Do I have it right or am I still missing something?

The re-alignment of the spacetime axes of the traveling twin resolves the twin paradox. But I realize I still have a hole in my understanding. If any frame can be considered the stationary frame, is there some perspective in which the traveling twin could assume he was motionless for the whole trip and that the "stationary" twin went out and back? (By the way, I have seen a video that showed just that: the traveling twin stationary while the Earth moves back and forth and claiming that, since everything is relative, either viewpoint is equivalent.)

Could we redraw the Minkowski diagram from the traveling twin's point of view?

My own attempt at an answer is that, if you change your frame, you can't treat it as though you are motionless and everyone else changed frames. Even if you had an inertialess drive and could switch directions instantly, you could still tell that you changed direction and not the rest of the universe. And if you wanted to draw a Minkowsky diagram for the traveling twin, you would need two, one for each direction.

I can say those words, but I have to admit to not having an intuitive understanding of why it's true. My best guess is that maybe inertialess drives are impossible because it would create this very confusion. Someone who didn't see the inertialess drive activated wouldn't be able to tell if they just experienced a change in direction or the rest of the universe did, and the twin paradox would turn into a real paradox. You can't resolve it if everything is symmetrical. Everyone has to be able to agree that the traveling twin was the one who changed direction.

Corrections and clarifications welcome.

 

[Nugatory]

If any frame can be considered the stationary frame, is there some perspective in which the traveling twin could assume he was motionless for the whole trip and that the "stationary" twin went out and back?

There is such a frame, but it is not an inertial frame so none of the straightforward equations like the time dilation formula can be used to compare times registered by a clock at rest in that frame with times registered by the Earth clock.

The best way to understand what each twin sees is by working through the Doppler Effect explanation in the Twin Paradox FAQ: http://math.ucr.edu/home/baez/physics/Relativity/SR/TwinParadox/twin_paradox.html. Just imagine that each flash of light is actually an image reflected from the clock at the source (or equivalently, a radio message reporting the time on that clock when the message is sent). For simplicity, assume that the turnaround is instantaneous and happens between flashes (any other assumption complicates the picture but introduces no new physical insight).

 

[Nugatory]

My best guess is that maybe inertialess drives are impossible because it would create this very confusion.

No, you've been misled by people putting too much emphasis on the acceleration.

The acceleration is actually a red herring; the important point is that the two twins took different paths through spacetime and these paths had different lengths. The acceleration only comes into the picture because
1) We can't send the twins on two different paths between the separation and reunion events without accelerating at least one of them, so there's going to be some acceleration somewhere as we describe the thought experiment.
2) We can point to the acceleration and say "look, it's not symmetrical so there's nothing inherently paradoxical about them having different experiences" (but we're still left explaining why they do have different experiences, and the acceleration doesn't help with that).

"The traveller was subjected to an inertialess drive" works just as well as "the traveller was subjected to acceleration" for both 1 and 2.

As an aside, it is possible to do an acceleration-free version of the twin paradox. When gravity is involved, it is possible to send the twins on different paths through spacetime between the separation and reunion events without accelerating either twin. We usually don't introduce the problem that way because it requires some additional background on the relationship between gravity and acceleration, and je problem is already confusing enough.

 

[Bandersnatch]

If any frame can be considered the stationary frame, is there some perspective in which the traveling twin could assume he was motionless for the whole trip and that the "stationary" twin went out and back? (By the way, I have seen a video that showed just that: the traveling twin stationary while the Earth moves back and forth and claiming that, since everything is relative, either viewpoint is equivalent.)

Could we redraw the Minkowski diagram from the traveling twin's point of view?

You can be very insistent on doing that, and just put the entire path of the traveling twin on a straight line. But, as mentioned by Nugatory above, since the traveling is necessarily changing inertial frames, doing so introduces a discontinuity as shown on the second of the three graphs in the link below:
http://www.einsteins-theory-of-relativity-4engineers.com/twin-paradox-2.html
The discontinuity is there because the outbound and the inbound trips of the traveling twin are objectively different inertial frames, with non-zero relative velocity, so the graph showing them both on one straight line is just two different graphs glued together. Compare with the third graph in the link to see the situation from the inbound trip perspective. You should see the half that makes up the inbound part of the second graph.

 

[Freixas]

No, you've been misled by people putting too much emphasis on the acceleration.

Corrrection: My favorite version of the twin paradox involves no acceleration. I've read articles and watched videos that have reinforced that the fact that one twin experiences acceleration is not relevant. So, the people I've been paying attention to have not been misleading me. I have to take credit for that all by myself. :-)

If there were such a thing as an inertialess drive, could a traveler detect that he has changed directions (or re-aligned his spacetime axes) and not the rest of the universe (assuming the traveler had no idea if the drive had engaged or even that his ship carried an inertialess drive)? If so, how? Or am I asking some silly question?

What if a cosmic prankster put an inertialess drive on the Earth and pulled away from the twin on the ship and then turned around and came back. Would the ship twin be fooled or would he know that his Earth twin is the one who will be younger when they reunite?

Edit: I meant a version with three observers. not the more complicated one with gravity, which I have not seen.

 

[PeterDonis]

If there were such a thing as an inertialess drive, could a traveler detect that he has changed directions (or re-aligned his spacetime axes) and not the rest of the universe (assuming the traveler had no idea if the drive had engaged or even that his ship carried an inertialess drive)?

You're assuming that without the inertialess drive, the traveling can detect that he has "changed directions" and not the rest of the universe, presumably by feeling his own proper acceleration. But feeling proper acceleration does not, in itself, mean that it's you who have "changed directions" and not the rest of the universe. You only know that when you meet up with your twin and see that he has aged more than you. The same would be true if you used an inertialess drive.

 

[Dale]

He records the clock and then corrects the recording for light delay. I believe he sees the traveling twin's clock running slow by the same factor on each leg of the trip.

Yes, this is correct. By the way, the fact that you explicitly mention correcting for the light delay is an indication that you do have a grasp on some of the important issues that arise in SR.

The traveling twin corrects his recording for light delay. He also sees his stationary twin's clock running slower and by the same amount on each leg. However, at turn-around, he sees his twin's clock jump forward in time. Do I have it right or am I still missing something?

This question is not as straightforward as the previous one. The reason is as follows:

In the case of the stationary twin the correction for light delay is simple, the first postulate says that the speed of light in vacuum is equal to c in any inertial reference frame. However, the traveling twin's frame is not inertial so it is not clear how to correct the observations for the light delay. The simultaneity convention used above is what I call the naïve simultaneity convention, and it simply uses the momentarily co-moving inertial frame's definition of simultaneity. In the "gap" and in the "overlap" regions the speed of light is no longer c, in fact all speeds of all objects in those regions are undefined.

One alternative is to use radar coordinates, which avoids those problems and results in a non-inertial reference frame where the speed of light is still c at all events. However, the drawings are a little different and can be surprising:

https://arxiv.org/abs/gr-qc/0104077

Note, this is not the only alternative to the naïve simultaneity convention, but it is one that I personally like.

If any frame can be considered the stationary frame, is there some perspective in which the traveling twin could assume he was motionless for the whole trip and that the "stationary" twin went out and back?

Yes, the above paper shows things from the traveling twin's frame. However, regardless of who is considered "motionless" the traveling twin is always the non-inertial one and the stationary twin is inertial.

 

[Freixas]

I know I have two questions. Let me try to clarify the first.

I like the video transmission idea, with corrections for light delay. That means that one can't really review the video until the trip is complete. The trip takes 10 years for the Earth twin, 6 for the traveling twin. The traveling twin always sees his Earth twin's clock running slow at a constant rate. Therefore, the traveler has a video recording 6 years long that shows less than 6 years passing on Earth. But the recording shows Earth 0 and the start and Earth 10 at the end. So, to my simplistic mind, the video should show a discontinuity.

If instead of a constant velocity and an inertialess turn-around, we use more typical acceleration, we can steal this diagram from Wikipedia:

This one show simultaneity from both viewpoints. Between traveling twin's years 4 and 5, it looks like time would appear to be running faster for the Earth twin than the traveling twin.

Dale just posted something that might affect my interpretation (about adjusting for light delay). The paper he refers to is rather advanced for me, but perhaps it addresses the question--I'm not sure.

 

[Freixas]

However, the traveling twin's frame is not inertial so it is not clear how to correct the observations for the light delay.

Let's say that we use this magic inertialess drive that people say it's OK to use. The traveling twin never accelerates or rather, the only acceleration is a change in direction at turn-around. Otherwise, he moves at a constant velocity. Can we now say that the traveling twin's frame is inertialess and so we can correct for light delay just as on Earth? Or do I not understand what you mean when you say the traveling twin's frame is not inertial?

Or we could just use two travelers, one outbound, one inbound, traveling at constant speed relative to Earth, who meet at the destination point. Outbound traveler passes inbound traveler the video he's recorded so far. Inbound traveler continues the recording. In this scenario, the gap is a lot less disturbing. Looking at it this way, it does seem that if we use the magic inertialess drive, there will be a gap and if we use conventional acceleration, the traveler will see the Earth clock run faster as he turns around.

But, hey, I've been wrong before. :-)

 

[Ibix]

Let's say that we use this magic inertialess drive that people say it's OK to use. The traveling twin never accelerates or rather, the only acceleration is a change in direction at turn-around. Otherwise, he moves at a constant velocity. Can we now say that the traveling twin's frame is inertialess and so we can correct for light delay just as on Earth? Or do I not understand what you mean when you say the traveling twin's frame is not inertial?

The problem is that it's non-trivial to correct for light travel time near the turnaround. You can't use the distance traveled by light from the outbound frame because that's wrong for the inbound frame due to length contraction, and vice versa. And because the two frames don't agree on what "at the same time as the turnaround" means there's no unique way to work out for what events you should use which frame.

One neat solution is Dolby and Gull's radar coordinates, which Dale linked above.

 

[Dale]

Let's say that we use this magic inertialess drive that people say it's OK to use.

I don't agree that it is OK to use in SR. You could use gravity to do it, but then you would need to use GR.

 

[PeterDonis]

do I not understand what you mean when you say the traveling twin's frame is not inertial?

This. In the presence of an "inertialess" drive, you have to be more careful in defining what an "inertial" frame is, but you can still do it based on properties like the behavior of light signals. For example, at the "turnaround", the traveling twin sees the Doppler shift of light signals coming from the stay-at-home twin change abruptly (instantaneously if the turnaround is like the diagram in post #1; over a finite interval of time if the turnaround is like the diagram in post #8) right when the turnaround happens. But the stay-at-home twin only sees the Doppler shift of light signals coming from the traveling twin change much later. (The article @Nugatory linked to in post #2 goes into this.) Going into this in more detail would require defining "inertial frame" in terms of the underlying flat spacetime geometry, which might be a bit too complex for this discussion. But it can be done.

In this scenario, the gap is a lot less disturbing. Looking at it this way, it does seem that if we use the magic inertialess drive, there will be a gap and if we use conventional acceleration, the traveler will see the Earth clock run faster as he turns around.

You don't need an "inertialess drive" or conventional acceleration to "turn around" in this scenario. The outbound traveler could send the inbound traveler his video using light signals; the inbound traveler just loads the received data into his own video camera and goes on from there. The video will show the Doppler shift of light signals arriving from Earth changing abruptly (as described above) either way.

Also, the "gap" you speak of is not something that's directly observed at the turnaround. It's something that has to be constructed from the data, and that construction requires assuming a simultaneity convention. In other words, the "simultaneity planes" drawn in the diagrams in posts #1 and #8 are not something anyone directly observes; they're constructions from the data, and the way they're drawn in those posts is not the only way to construct them.

One big advantage of the Doppler shift approach (described in the article @Nugatory linked to, and which I've briefly described here) is that it doesn't require any such constructions. It doesn't even require a simultaneity convention. It just focuses on the differences between what the two twins actually see (as in, observe directly with their eyes and instruments) to explain why their clocks read different elapsed times when they meet up again. And this way of doing the analysis doesn't even care how, physically, the turnaround is accomplished, or about "frames" or anything else. You could work things out the same way using the Doppler shift approach if the traveling twin used a distant planet as a gravitational "slingshot" to reverse course (meaning he would feel zero acceleration even without having to use an inertialess drive).

 

[PeterDonis]

I don't agree that it is OK to use.

It's unphysical, yes, but I think it's fair to emphasize the point that how, physically, the turnaround is accomplished, including whether the traveling twin feels acceleration during it, is irrelevant to the calculation of differential aging.

 

[Ibix]

I don't agree that it is OK to use.

You can make the acceleration phase negligible, however, just by increasing the distance traveled to tens of thousands of light years. You can accelerate to relativistic speeds in a year or so at relatively sedate accelerations.

That said, I agree with you. The point is that the traveling twin is not at rest in a single inertial frame. "Inertialess" in the E.E. "Doc" Smith sense of being able to stop and maneuver instantaneously is just confusing in this context, to my mind. Not to mention probably unphysical (what do I mean by "stop" for example?)

 

[Dale]

It's unphysical, yes, but I think it's fair to emphasize the point that how, physically, the turnaround is accomplished, including whether the traveling twin feels acceleration during it, is irrelevant to the calculation of differential aging.

I don't like it, because to me more fundamental than all of SR is being able to identify an inertial frame from a non-inertial frame. Allowing non-physical inertialess drives destroys that. Since that is more basic than SR, then I am not willing to entertain it as anything other than sci-fi entertainment.

 

[PeterDonis]

I don't like it, because to me more fundamental than all of SR is being able to identify an inertial frame from a non-inertial frame.

This is a fair point. I think such a definition can still be formulated based on spacetime geometry, as I mentioned before, but I agree that allowing an inertialess drive basically removes the physical connection between the motion of objects and spacetime geometry, so it puts the latter on a much shakier foundation.

 

[Dale]

@Freixas as @PeterDonis indicates, an inertialess drive is unphysical. I would not pursue it too much. If you already know what you are doing, then you can carefully formulate the twins scenario correctly (see post 12). However, if you do not already know what you are doing, then you are likely to get things wrong. I most emphatically recommend that you not pursue it further until you have mastered special relativity and at least begun general relativity. You should (IMO) not begin this until you can understand the first two chapters of Sean Carroll's "Lecture Notes on General Relativity".

I will not answer any questions based on a non-physical inertialess drive.

 

[Dale]

You can make the acceleration phase negligible, however, just by increasing the distance traveled to tens of thousands of light years. You can accelerate to relativistic speeds in a year or so at relatively sedate accelerations.

Yes, or you can just use "future technology" to allow arbitrarily high accelerations. A sharp turnaround is OK to me, but I just want to make sure that accelerometers still detect the acceleration.

 

[Freixas]

One alternative is to use radar coordinates, which avoids those problems and results in a non-inertial reference frame where the speed of light is still c at all events. However, the drawings are a little different and can be surprising:

https://arxiv.org/abs/gr-qc/0104077

The radar approach doesn't seem to forbid the speed-up. I have to confess that most of the paper makes my eyes glaze over, so I can't be sure what Figure 5 represents. In Region I, which appears to be the region I am most interested in, it sure looks like the lines of simultaneity (from Barbara's view) make it so that Alex's clock runs faster than Barbara's.

The thing that attracted my attention to this is that the first concept one hears is that each observer views the other's time as running slower., so it's only at the turn-around that I'm seeing cases where that's not so. Or appears not to be so.

As I am more an engineer than a mathematician, it seemed like recording the whole thing on video should make it all clear. Ibix said "The problem is that it's non-trivial to correct for light travel time near the turnaround." and Dale doesn't like inertialess drives. How about the following?

• B passes A at some constant velocity relative to A. A and B set their clocks to 0 as they pass. A begins to transmit video of his clock to B who records it for later.
• Some time later, B passes C, who is traveling towards A also at velocity v. B passes his video recording and clock time to C, who immediately begins his own recording of A's signal.
  
• C passes by A and passes his recording and clock time to A and continues on. Let's say this conjunction happens at time T. We expect that the time that C passes to A will be T', where T' < T.
  
• As both A and C were traveling at constant speed, A can calculate the light delay for every frame and adjust as needed. To make this easier, every frame embeds A's time and the recording medium records the local time at which it was received.

Well, maybe I'm wrong about how easy it is to calculate, but there seem to be a lot of articles which claim that it can be done (the Wikipedia page, for one). Nobody is accelerating and nobody changes their frame of reference at any point.

I sit down at a theater to watch this fascinating video. What do I see? I mean, I will see something, right? I know the recording starts with a clock showing 0 and ends with a clock showing T. The length of the recording can't exceed T'. T seconds over a period of T' (where T' < T) would suggest that B and C perceived A's clock as running fast at some point (or the tape had the equivalent of an "intermission").

Note that I am not drawing any simultaneity planes (at least, I don't think I am). I am just watching a video. The only adjustments made to the video were for light delay.

There could be a lot of ways to answer this that avoid talking about what the video shows. The video creation assumes that you can adjust for light delay. Everyone in this scenario is moving at constant speed, so that seems to me to be reasonable, but if it's not, let me know. Other assumption about passing clocks and videos across at conjunction don't seem completely out of line, at least not for these kinds of thought experiments, but if that's flawed, go ahead and point it out. However, assuming that the problem is set up properly, the answer I'd interested in is about what the video would show.

As it doesn't appear there would be any discontinuity in the video (C picks up right where B left off). I suspect the problem is that C is picking up video that really was intended for B, so that the correction for light delay gets processed in the wrong reference frame and that somehow skews the result. I still wouldn't mind knowing what the video would show. I'd love to calculate it myself, but I'm more likely to write a software simulation and then see what happened.

 

[Ibix]

Depends what they do with the video.

The problem with this set up is that video cameras produce 25 images per second in their rest frame. Each video image will therefore show the clock one twenty fifth of a second advanced from its previous state, because the clock being videoed and the clock controlling the camera shutter are at rest with respect to one another.

Due to the increasing distance between A and B, B will wait a long time between receiving successive images. Due to the decreasing distance between A and C, C receives images at very short intervals.

What you see when you watch it then depends on how you interpret those incoming images. Do you show them at the spacing you received them? In that case you get the same effect as an old hand-cranked projector that is turning very slowly for half the journey and then super quickly for the second half. Or do you show them every 25th of a second? In that case you just see an ordinary video of a clock - the only odd thing is that (by B and C's combined wristwatches) they were away for a year but have two years' of footage, because A says the trip took two years and it's A's clock that dictates how many images were sent.

 

[PeterDonis]

As I am more an engineer than a mathematician, it seemed like recording the whole thing on video should make it all clear.

The Doppler shift explanation that @Nugatory linked to describes exactly what such a video, recorded as you describe, would show--the only caveat is that it describes what the "raw" video, without any "correction for light travel time", would show.

I'm not sure how you would "correct" the actual video for light travel time. You could certainly calculate, from the raw data provided in the video (in particular the clock readings and Doppler shifts observed), a "light travel time corrected" time for various events. But any such calculation requires adopting a simultaneity convention; there is no way to make the calculation just from the data in the video.

I suspect that your confusion is largely being caused by a failure to properly appreciate the point made in the last paragraph. It is a somewhat subtle point, and is not well explained even in most textbooks on SR, so unfortunately it's not surprising that many people have trouble with it. But that doesn't make the point any less valid.

 

[PeterDonis]

I am not drawing any simultaneity planes (at least, I don't think I am). I am just watching a video. The only adjustments made to the video were for light delay.

As I said in my previous post: adjusting for light delay requires adopting a simultaneity convention. So you are drawing simultaneity planes here; you just don't realize it.

 

[Dale]

The radar approach doesn't seem to forbid the speed-up.

I don’t know what you mean by “forbid the speed-up”. It

1) keeps a non inertial object at rest
2) is a mathematically valid coordinate chart
3) allows the speed of light in vacuum to remain c

I can't be sure what Figure 5 represents. In Region I, which appears to be the region I am most interested in, it sure looks like the lines of simultaneity (from Barbara's view) make it so that Alex's clock runs faster than Barbara's.

Yes, you are correct.

The thing that attracted my attention to this is that the first concept one hears is that each observer views the other's time as running slower.,

Remember, that is for inertial frames, and Barbara’s frame is not inertial. In her frame Alex’s clock runs fast in region 1.

Nobody is accelerating and nobody changes their frame of reference at any point.

There are three relevant inertial frames in this scenario. Certainly there is nothing wrong with using three inertial frames, or one inertial and one non-inertial frame.

A can calculate the light delay for every frame and adjust as needed

Ok, that is fine, but then it is A’s simultaneity. The resulting video will not be anyone’s frame. It will have space according to B or C and time according to A.

I sit down at a theater to watch this fascinating video. What do I see? I mean, I will see something, right? I know the recording starts with a clock showing 0 and ends with a clock showing T. The length of the recording can't exceed T'.

You will see A’s clock go away and come back, all the while ticking at a steady 1 s per s. The recorded local time will go more slowly.

Note that I am not drawing any simultaneity planes (at least, I don't think I am).

They are implicit in the correction for light delay. Since A is doing that correction then it is A’s simultaneity.

The video creation assumes that you can adjust for light delay.

Certainly you can do so but the result is frame variant.

As it doesn't appear there would be any discontinuity in the video (C picks up right where B left off).

Correct. There is no discontinuity in the raw footage. There is also no discontinuity introduced if either A or B or C does all of the light delay correction. The only way a discontinuity is introduced is if B does the light delay correction for the first half of the video and C does the second half.

 

[Freixas]

Hey, everyone, thanks so much for your corrections.

@PeterDonis: Yes, silly me, I am relying on simultaneity planes from B's and C's frame.

@PeterDonis: "The Doppler shift explanation that @Nugatory linked to describes exactly what such a video, recorded as you describe, would show--the only caveat is that it describes what the "raw" video, without any "correction for light travel time", would show." Yes, I am familiar with those uncorrected videos. I've seen them described in several places including the Wikipedia page I mentioned. At this point, I could probably tell you, by heart, what an uncorrected video would show for a commonly used case (5LY trip at 0.8c).

@Dale: Not sure why Barbara's frame is non-inertial in Figure 5. The way that Barbara's lines are drawn implies constant velocity except at the instant of turn-around. Am I reading that graph incorrectly? I thought Figure 6 was the non-inertial case.

@Dale: You verified that Alex's clock can run faster than Barbara's. Thanks! This is one of the key points I wanted verified because I generally only hear about Alex's clock running slower, so I thought maybe I misunderstood. I've seen at least one other reference that specifically mentions a clock running faster in the twin paradox, but can't find it again.

@Ibix: Actually (and as PeterDonis pointed out), the final spacing of the video frames will be based on B's and C's calculations of when the video frame was sent, corrected by them for light delay.

@PeterDonis: You say you are not sure how the frames could be corrected for light delay. Well, then, wouldn't that be an interesting problem to tackle? :-)

The whole video idea is just me trying to see if we could actually view simultaneity planes in action. I said I was more engineer than mathematician, so I my instinct is to try to see the simultaneity described by the simultaneity planes. Light delays are unavoidable, but make direct viewing impossible. So, of course, I try to engineer a solution that removes the light delay. If the frames could be corrected by simply calculating, on receiving a frame, where I was when it was sent, then at first blush it appears we could view the simultaneity in action.

I realize it's probably not that simple, which is why I need to take some time to work through the problem. I did want to get back to everyone who took time to participate, though. It's much appreciated.

 

[Nugatory]

Not sure why Barbara's frame is non-inertial in Figure 5. The way that Barbara's lines are drawn implies constant velocity except at the instant of turn-around. Am I reading that graph incorrectly?

There is no single frame in which B is traveling in a straight line at constant velocity for the entire journey; therefore the frame in which B is at rest for the entire journey is not inertial. There is an inertial frame in which B is at rest for the first half of the the journey and moving during the second half and there is an inertial frame in which she is moving in the first half and at rest in the second half (the Earth is moving in a straight line at a constant speed in both of these frames, although in different directions).

 

[Ibix]

@Ibix: Actually (and as PeterDonis pointed out), the final spacing of the video frames will be based on B's and C's calculations of when the video frame was sent, corrected by them for light delay.

You'll note that I said

Depends what they do with the video.

If they respect the times implicit in the video format then they get an absolutely uninteresting video that they don't have time to show in the trip. If they display the images as they come in they get Doppler shifted video.

 

[PeterDonis]

You say you are not sure how the frames could be corrected for light delay. Well, then, wouldn't that be an interesting problem to tackle? :-)

When I said "I'm not sure", I meant that you did not give, in your statement of the scenario, enough information to know how you would make the correction. But giving that information is just a matter of telling us what simultaneity convention you are using. Once you've done that, the "problem" is solved; there's nothing to tackle. And since simultaneity is a convention, there's nothing to "solve" there either; you adopt whatever convention works best for you.

The whole video idea is just me trying to see if we could actually view simultaneity planes in action.

That's easy: you can't. Simultaneity planes aren't things you can "view". They're conventions. This is like trying to see if you could actually view latitude and longitude coordinates on the Earth's surface "in action". You don't "view" these things, you use them as tools.

 

[PeterDonis]

Light delays are unavoidable, but make direct viewing impossible. So, of course, I try to engineer a solution that removes the light delay.

Light delay makes direct viewing of a distant object impossible. But direct viewing of an object is not the same as direct viewing of a simultaneity plane. Simultaneity planes aren't objects. They're abstractions. They're human conventions.

Engineering a solution that removes the light delay could be a way of trying to see what is happening to a distant object "in the distant object's rate of time flow", so to speak. But again, that's not viewing a simultaneity plane; it's just viewing the distant object with a correction for light delay.

 

[Dale]

The way that Barbara's lines are drawn implies constant velocity except at the instant of turn-around. Am I reading that graph incorrectly?

You are reading it correctly, but misunderstanding what “inertial” means. To be inertial it must be constant velocity. No exceptions. Constant velocity except at an instant turnaround is non inertial.

I thought Figure 6 was the non-inertial case.

Both figures show Barbara as non inertial. Figure 6 is just a more realistic worldline.

 

[Freixas]

Depends what they do with the video.

The problem with this set up is that video cameras produce 25 images per second in their rest frame. Each video image will therefore show the clock one twenty fifth of a second advanced from its previous state, because the clock being videoed and the clock controlling the camera shutter are at rest with respect to one another.

Due to the increasing distance between A and B, B will wait a long time between receiving successive images. Due to the decreasing distance between A and C, C receives images at very short intervals.

What you see when you watch it then depends on how you interpret those incoming images. Do you show them at the spacing you received them? In that case you get the same effect as an old hand-cranked projector that is turning very slowly for half the journey and then super quickly for the second half. Or do you show them every 25th of a second? In that case you just see an ordinary video of a clock - the only odd thing is that (by B and C's combined wristwatches) they were away for a year but have two years' of footage, because A says the trip took two years and it's A's clock that dictates how many images were sent.

I should have posted a correction to this earlier. Neither of the options you mentioned is the one I was thinking of. B receives a frame from A and completely ignores the contents. He calculates how long it has been traveling away from A. Then he places the frame in a new video, where the time at which the frame is positioned is B's current time minus how long it has been traveling. This is the correction for light delay.

Now B says: "At the same time that we were X days from our conjunction with A, A sent this frame." This seems to me where I am assuming something about simultaneity. My theory was that this would reflect the simultaneity planes that I usually see to illustrate time dilation. But apparently not. What I mean is that I ran through some numbers and the results didn't match.

So my process for correcting for light delay is flawed and the intuitive feeling that we could use it to "view" simultaneity is wrong.

While I would appreciate an explanation, I'm not sure you guys would be able to provide one even with the best intentions. I just took a look at Carroll's first two chapters in Lecture Notes on General Relativity. If understanding that is what it takes, then it's definitely not going to happen. I'm not 100% sure that my mistake couldn't be explained to me in a way that I could understand, but I'm not 100% it could, either.

I mentioned numbers and so I should provide them. I am only going to look at A and B just to avoid muddying up anything with non-inertial frames and turn-arounds.

B is traveling at 0.8c relative to A. Let's place a marker M that is motionless relative to A and is 4 LY away from A. B sees this same distance as 2.4 LY and for him, it takes 3 years to reach M. For A, B takes 5 years to reach M. The video frame that B receives from A at M says 1 year. B calculates the travel time of the video frame (2.4 years) subtracts it from his clock (which reads 3 years) and thinks that A sent the video when B was .6 years on his journey. Since the frame reads 1 year, B thinks A's clock is running faster than his.

Reversing this for A: At year 9, A's time, he receives a video frame from B sent from point M with time 3 years. The frame traveled 4 LY, so A thinks it was sent when A's clock read 5 years. For A, B's clock is running slower. The numbers are actually what I expected (time dilation of 0.6).

Using this method, both agree B's clock is running at 0.6x that of A's clock, clearly a wrong conclusion. Even getting this wrong, I would have expected it to be wrong both ways—even more confusing.

 

[PeterDonis]

He calculates how long it has been traveling away from A.

How?

Now B says: "At the same time that we were X days from our conjunction with A, A sent this frame." This seems to me where I am assuming something about simultaneity.

No, you did it in the step before (that I quoted above and asked "how?"). You need to assume a simultaneity convention in order to calculate how long the light has been traveling. There is no absolute answer to that question; it is frame-dependent because time is frame-dependent (which is equivalent to being simultaneity convention dependent).

B calculates the travel time of the video frame (2.4 years)

This is an example of what I just said above. It's 2.4 years in B's frame, but not in A's frame. So the "how long" calculation itself is frame-dependent.

 

[Freixas]

This is an example of what I just said above. It's 2.4 years in B's frame, but not in A's frame. So the "how long" calculation itself is frame-dependent.

I would say, of course, that's the whole point. I am trying to calculate the light delay in B's frame. For example, astronomers see a star blow up and tell you that, although we see it happen now, it actually happened some calculable time in the past. All the calculations are in our frame--our distance to the star and our time line.

The mysteries of my approach are not just that I got what I think is a wrong answer, but that the answer is exactly the inverse of what I would expect (B thinks his clock runs 0.6 slower than A's), that the answer when looked at from A's point of view wasn't also reversed and that A's answer is what I would have expected.

I just remembered that one of my neighbors is a retired physics professor, so maybe I can get him to walk me through this. Thanks for your help, though.

 

[PeterDonis]

I am trying to calculate the light delay in B's frame.

Yes, but you are then combining it incorrectly with a clock time in A's frame, because you are leaving out relativity of simultaneity--or, to use the term that seemed to work better for you in another thread, clock offset.

Let me rephrase things explicitly from the point of view of B's frame:

A departs B at a speed of 0.8; both A's and B's clocks read zero. M is 2.4 light-years away and is moving towards B at the same speed, 0.8. But at this time in B's frame, M's clock does not read zero. It reads 3.2 years. (I'll leave it to you to figure out how to get that number; the easiest way to visualize it is to draw a spacetime diagram.)

3 years later by B's clock, M arrives at B. M's clock reads 5 at this event. That means that, in B's frame, during the time between meeting A and meeting M, M's clock ticked away 1.8 years. Since B's clock ticked 3 years, M's clock is ticking at a rate 1.8/3 = 0.6 relative to B's clock--precisely the expected time dilation factor. And since A's clock and M's clock are synchronized, A's clock must be ticking at the same rate.

At the same event where B meets M, B receives a light pulse from A showing A's clock reading 1 year. B correctly calculates that this light pulse took 2.4 years to travel according to his frame. [Edit--this is incorrect--see follow-up post #34.] However, in order to calculate how fast A's clock is ticking relative to his own, he has to know what event on A's worldline is simultaneous, in his frame, with the event where he meets M, and what A's clock reads at that event. The light pulse's travel time in B's frame does not give any information about that. In fact, the single light pulse itself is irrelevant to the calculation of A's tick rate during the time between the two meetings.

The correct answer is that A's clock reads 1.8 years at the event on A's worldline that is simultaneous with B meeting M (note that this calculation is very similar to the calculation above that told us that M's clock reads 3.2 years at the event on M's worldline which is simultaneous, in B's frame, with B and A's meeting); and, again, that means A's clock ticked 1.8 years while B's clock ticked 3 years, just like M's clock, so again we get the expected time dilation factor of 0.6.

In other words, the short answer is that, if all you have is a single light pulse showing a single reading of A's clock, you cannot tell anything about the tick rate of A's clock relative to B's clock. You need at least two light pulses, if light pulses are what you want to use.

 

[PeterDonis]

B correctly calculates that this light pulse took 2.4 years to travel according to his frame.

Actually, this is wrong! See below.

the short answer is that, if all you have is a single light pulse showing a single reading of A's clock, you cannot tell anything about the tick rate of A's clock relative to B's clock.

Actually, this is a bit pessimistic. We can use the light pulse's travel time in B's frame if we figure out at what time, in B's frame, the pulse was emitted. In other words, we need B's clock reading at the event on B's worldline which is simultaneous with A's emitting the light pulse (when A's clock reads 1). That is not the event at which B's clock reads 0.6 (which is what your calculation implicitly assumed)--that event is simultaneous to A's clock reading 1 in A's frame, not B's frame. (This is why I said in my previous post that your calculation failed to take clock offset into account.)

If we run the numbers, we find that the time, in B's frame, when A emits the light pulse (i.e., when A's clock reads 1) is 5/3 (fractions turn out to be easier than decimals for these numbers). In other words, this time is 4/3 earlier than the time B meets M (which is time 3 by B's clock). Which in turn means that the light pulse took 4/3 years to travel, not 2.4 years, so it covered 4/3 light years, not 2.4 light years.

Where did we go wrong before? By assuming that, since M is 2.4 light years from B when B meets A, A must be 2.4 light years from B when A emits the light pulse that arrives at B when B meets M. But that is not valid logic. The only valid reasoning we can do to obtain the distance the light pulse covered is the reasoning I did above, which starts from A's known clock reading when the light pulse was emitted and calculates what B's clock read at the same time, in B's frame, as that emission event. And, of course, knowing that the light pulse covered 4/3 light years, we can see that A, traveling at speed 0.8, took 4/3 divided by 0.8 = 5/3 years in B's frame to travel from A's meeting with B to the point where the light pulse was emitted--and we already saw above that the time of emission, in B's frame, was 5/3 years. So A's clock ticked 1 year while 5/3 years elapsed in B's frame, for a time dilation factor of 0.6, again as expected.

 

[PeterDonis]

you are then combining it incorrectly with a clock time in A's frame, because you are leaving out relativity of simultaneity--or, to use the term that seemed to work better for you in another thread, clock offset.

Actually, this was a bit pessimistic too. With the correct light travel time in B's frame--4/3 years--you can indeed subtract that time from 3 years (B's clock reading when he receives the light pulse), obtain 5/3 years for the time of emission according to B's frame, and compare that with A's clock reading of 1 year shown in the video frame to obtain the correct time dilation factor of 0.6, as I showed in the previous post.

The miscalculation of the light travel time as 2.4 years is really more a matter of not realizing that A is 2.4 light years from B when B receives the light pulse, not when A emits it, because A is moving away from B while the light travels.