Sine wave with variable frequency

[kvtb]

I'm trying to do something very simple...
I'd like to have a sine function, where the frequency is controlled by a separate frequency function

Something like this:

g(t) = sin(2*pi*f(t)*t)

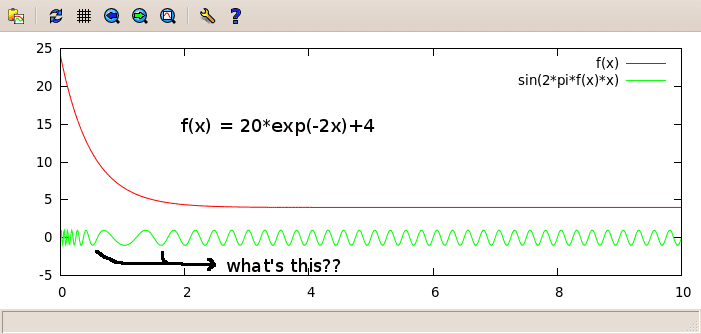
Assume that
f(t) = 20*exp(-2*t)+4

I would expect a sine wave that starts at 24 Hz and then slowly slows down to 4 Hz.
But when I plot it, I get some strange results for t in [0.5, 2], see attached image. The frequency for those values is very low. How's that possible? Is it my plotting program that acts funny? How can I get the expected (described) behaviour?

Thanks in advance!

 

[flatmaster]

does your program think that the angle your inputing into your Sin function is in Radians, or degrees?

 

[es1]

I haven't done this myself yet but I suspect when you expand from exp to trig form you'll find you have a beat.

20*exp(-2*t) is about 4 around t=0.8.

http://en.wikipedia.org/wiki/Beat_(acoustics )

 

[Redbelly98]

This is weird. Do you still get this effect if you zoom the plot to 0.5<x<2?

does your program think that the angle your inputing into your Sin function is in Radians, or degrees?

It looks like the software (mathcad?) is correctly interpreting the sine argument as radians, as evidenced by the 4 Hz oscillation for x>2.5.

I haven't done this myself yet but I suspect when you expand from exp to trig form you'll find you have a beat.

20*exp(-2*t) is about 4 around t=0.8.

http://en.wikipedia.org/wiki/Beat_(acoustics )

This does not look like beating, the amplitude stays constant.

 

[Redbelly98]

Update: I plotted this function in Excel, and get the same plot! I'm looking more closely at this, stay tuned.

 

[flatmaster]

Perhaps using the same x in the f(x) expression and Sin expression is confusing. I would try to explicitly plug in your exponential f(x) into one long expression as a function of x only. Don't forget brackets around your f(x) expression so it distributes correctly.

 

[Redbelly98]

Okay, I have figured it out.

Generally, we have

y = sin[θ(t)]​

I.e., the argument of the sine can be thought of as a time-dependent phase angle.

The angular frequency is

ω = dθ/dt​

Differentiate the sine argument in the OP, and one finds

ω ≠ 2π f(t)​

 

[es1]

I am not sure I follow RedBelly98. I think you need an explanation for why the frequency is lower than 4 in the range 0.5 to 1.5. I think the only explanation is there must be positive interference between the two frequencies, which would be a beat. But I could be wrong.

I think you can expand:

Sin(2pi(20Exp(-2t)+4)t) = 2Cos(pi(20Exp(-2t)t+pi4t)Sin(pi(20Exp(-2t)t+pi4t) = 2Cos( (f1-f2)/2 t)Sin( (f1+f2)/2 t)

Then solve for f1 and f2 (assuming there is a solution which is why I could be wrong).

I suspect it's right because 20Exp(-2t) is about 4 near 1 so one would expect the beat frequency to be very low around this number which is also what we observe in the plot.

It's not in the range -2,2 like in the wikipedia article because the original function was wrapped in a sine which scaled it to the range -1,1.

 

[es1]

Also, it seems the amplitude is not necessarily constant.
Try altering the function slightly,
Sin(2pi(40Exp(-2t)+4)t)
this amplitude is definitely not constant.
Darn, I might have to find some time to try to solve this one... :)

 

[elibj123]

What RedBelly was saying is that the extension from constant to varying frequency is not done by multiplication but differentiation.

Just like the differential slope of a curve A(t)*t is not A(t) but [A(t)*t]' (I wrote the function in this form to deliver the point)

The "differential frequency" of a sine wave, is the derivative of its argument rather than the coefficient of t.

Try plotting the function sin(-10*exp(-2t)+4t) and check if it gets you the desired result.

 

[Redbelly98]

I am not sure I follow RedBelly98.

Okay. Suppose we have a spinning object, and we are given it's orientation θ as a function of time, not necessarily a linear function. How would you determine the rotation rate, ω?

I think you need an explanation for why the frequency is lower than 4 in the range 0.5 to 1.5.

You differentiate the sine argument in the OP,

2π*[20*exp(-2*t)+4]*t​

and find that the result is less than 2π*4 rad/s, or 4 Hz, over some range.

 

[kvtb]

Hi, thanks for your replies.

Very interesting discussion.

When I plot sin(2*pi*(-10*exp(-2t)+4t)), I get exactly what I want/expected.

But... elibj123, how did you get to this: -10*exp(-2t)+4t ?
When I calculate [f(x)*x]' I get something else, namely:
-40\,x\,{e}^{-2\,x}+20\,{e}^{-2\,x}+4

edit: aaah, it is the antiderivative of f(x)! :-)

 

[es1]

Ok. I get the phase and phase velocity argument. That makes a lot of sense.

When I take the derivative I find that the min frequency is at t=1 and the phase velocity is ~1.3 which matches the plot very nicely.

Thanks.