- #1
dvep
- 43
- 0
Homework Statement
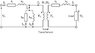
Figure 1 shows the equivalent circuit of a single phase transformer and figure 2 shows the approximate equivalent circuit.
Reduce the circuit to approximate form and find:
rm, xm, R1, X1
Using the approximate equivalent circuit calculate-
With the transformer operating at no-load:
primary current , primary power factor, primary real power, secondary voltage.
I am given in the equivalent circuit:
r1, r2, rm, x1,x2,xm, turns ratio, V1
Homework Equations
R1 = r1' + r2'
X1 = x1 + x2' = x1 +x2(N2/N1)
The Attempt at a Solution
Using the equations above I have found R1 and X1
I now need to find rm and xm of the approximate equivalent circuit and primary current , primary power factor, primary real power, secondary voltage.
I am struggling with this, any help would be appreciated, thankyou.
Attachments
Last edited: