Sinusoidal steady state circuit

[magnifik]

I am trying to find the indicated currents for the following circuit, given v1 = 2sin(2t + 45):

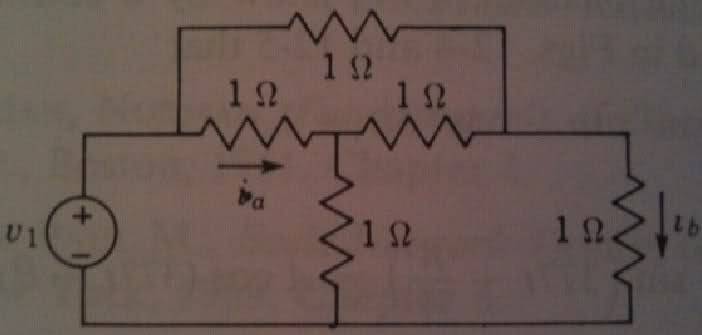
I attempted to solve it in the following way:
v1 = 2sin(2t+45) // given
= 2[sin(2t)cos(45) + cos(2t)sin(45)]
= √2[sin(2t) + cos(2t)]

I use a matrix for the loops:
A =
[2 -1 -1
-1 3 -1
-1 -1 3]

b =
[√2
0
0]

I'm wondering what format the final solution should be in. Should it be Isin(2t+45) or I[sin(2t) + cos(2t)]?

Btw, I got √2/2 for the magnitude of both the currents.
Any input is appreciated. Thanks in advance.

 

[gneill]

Since the network is purely resistive it won't muck about with the current phase anywhere in the circuit. So I'd solve for the currents as though it were a DC source of 2V. Tack the sin(2t+45) back onto the results you get and call it a day!

 

[magnifik]

Since the network is purely resistive it won't muck about with the current phase anywhere in the circuit. So I'd solve for the currents as though it were a DC source of 2V. Tack the sin(2t+45) back onto the results you get and call it a day!

ok. thank you.

 

[magnifik]

I got 1 as the magnitude for both of the currents so i = sin(2t + 45)

 

[gneill]

I got 1 as the magnitude for both of the currents so i = sin(2t + 45)

I find that I_a is not the same as I_b. Perhaps you can check your matrix calculation?

 

[magnifik]

I got I1 = 2, I2 = 1, I3 = 1
where I1 is the current in the loop on the left part of the circuit, I2 is the current in the top part of the circuit, and I3 is the current in the loop of the right part of the circuit.

Ia = I1-I2 = 1
Ib = I3 = 1

 

[gneill]

I got I1 = 2, I2 = 1, I3 = 1
where I1 is the current in the loop on the left part of the circuit, I2 is the current in the top part of the circuit, and I3 is the current in the loop of the right part of the circuit.

Ia = I1-I2 = 1
Ib = I3 = 1

Yes, you're right! I was thinking that Ia was the current from the supply. I must be getting tired