bd411
- 39
- 0
Homework Statement
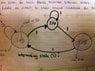
Sketch the moore state diagram for the circuit shown in the figure, where A is the input variable. You may assume initially that Q[2:0] = 000.
CLK = clock.
The box with the & inside is an AND gate.
Q[2:0] means that initially Q0, Q1, and Q2 = 0 and hence there inverses are equal to one.
Homework Equations
None.
The Attempt at a Solution
I understand the layout of the Moore diagram, a bubble for each state, with a slash and the corresponding output next to it.
XX / XX
STATE NUMBER
OUTPUT OF THAT STATE
Furthermore, an arrow is used to represent all possible transitions between states and the labels on the arrows show the required conditions for the transit.
What I am having issues with is actually drawing the diagram. Supposing A = 0, when the first clock pulse arrives, Q2 will still be 0. This will happen continuously as long as A = 0.
The difficulty arrives when we set A=1, then as far as I can see the output of Q2 will STILL be 0 ? Do I represent this as an intermediary state, with output still 0 as was the output of Q2 was in state 1, or just draw an arrow from state 1 to itself ?
Supposing the next A=1 is input at the clock pulse, will the output of Q2 STILL not be 0? (as the one hasn't travlled through the circuit yet). Once again, intermediary state ? I believe that at the next A = 1 clock pulse the output of Q2 will be 1.
Supposing another A = 1 (this time K=1 too), the output of Q2 will now be 0 again.
I haven't even considered instances where a 1 is followed be a 0, or 2 1's are followed be a 0. I feel like I am thoroughly overcomplicating this problem and any guidance will be very much appreciated !
I have attached the question and my partial solution.