- #1
Hereformore
- 61
- 0
I'm a little confused as to the conceptual premise behind torque-ladder problems? Like "at what height up the ladder is the man and ladder most likely to slip?"
I understand how to solve such problems, but i have trouble understanding how it is a torque problem.
Is it a torque problem or rather a static equilibrium problem? I know they're kind of the same thing, but as a torque problem, I can't imagine the object actually rotating. Rather i imagine it slipping but once it starts slipping the torque conditions constantly change as the angle theta of the ladder against the ground changes.
As an equilibrium problem, it makes sense because in static equilibrium using torue allows us to use more information to understand the force interactions.
Am I "right" in being confused about this as a traditional torque problem?
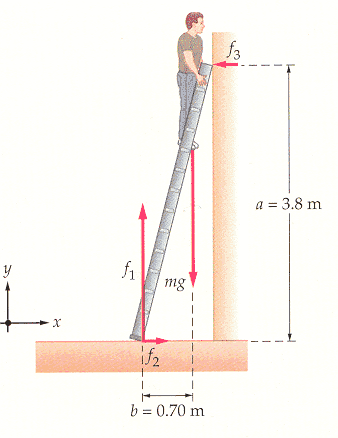
I understand how to solve such problems, but i have trouble understanding how it is a torque problem.
Is it a torque problem or rather a static equilibrium problem? I know they're kind of the same thing, but as a torque problem, I can't imagine the object actually rotating. Rather i imagine it slipping but once it starts slipping the torque conditions constantly change as the angle theta of the ladder against the ground changes.
As an equilibrium problem, it makes sense because in static equilibrium using torue allows us to use more information to understand the force interactions.
Am I "right" in being confused about this as a traditional torque problem?