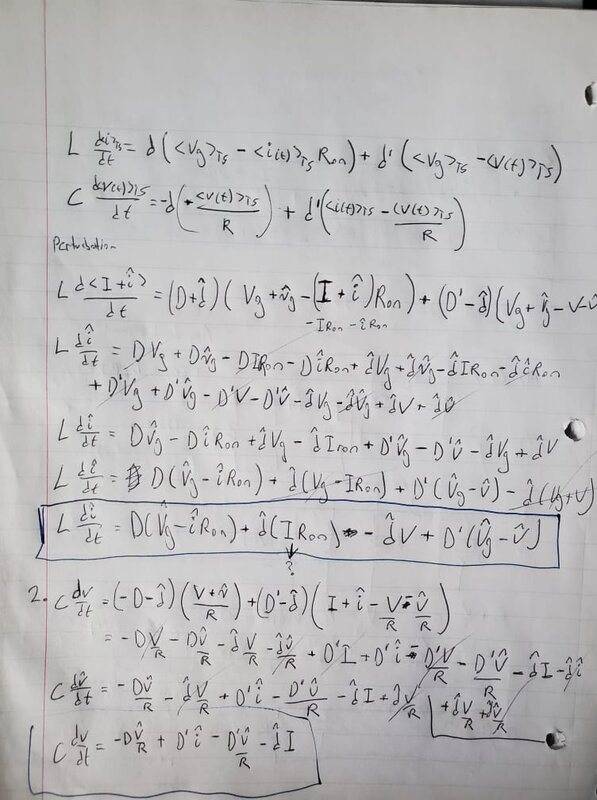Small signal AC modeling for a boost converter with resistive losses

[pjcircle]

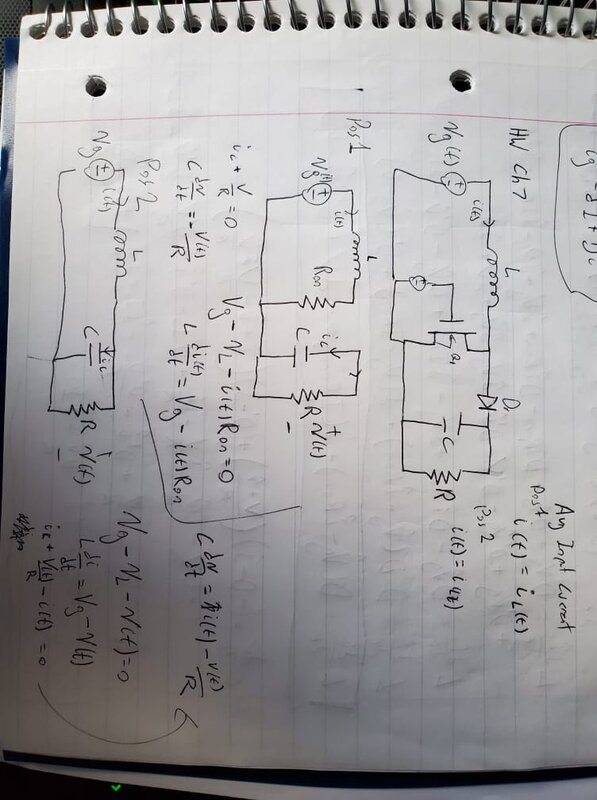
Homework Statement

Derive the small signal equations associated with both the capacitor and inductor.

Relevant Equations

L dihat/dt=RHS
C dvhat/dt=RHS

I've attached my attempts at the solution and the actual question below. I believe the only issue I am having is I don't know how to get rid of "I" in both my final inductor and capacitor equations as the HW states I shouldn't have anything in term of I. I believe I need to put "I" in terms of the listed variables but I cannot for the life of me figure out how to do it. In the lectures and textbook that come with this HW they do actually leave the solution with terms that include "I" which is a bit frustrating. I already removed the second order and DC quantities as can be seen in the work but "I*Ron*dhat" and "dhat*I" are first order factors that should not be removed. The blue boxed in equations in third image are my incorrect answers for #1 and #2.

 

[alan123hk]

I did not study your derivation process in detail. However, I think in a sense, you can’t get rid of "I". The small-signal AC model of the boost converter must actually include the influence of the quiescent inductor current, but, as mentioned in the HW, according to the steady-state model, you should be able to use other parameters to represent it. You may try to consider whether this quiescent inductor current is related to, for example, the output voltage and some other parameters?

 

[Henryk]

I don't think your equations are correct. First of all, since the convertor operates in continuous current mode, the average (over a switching period) inductor current equals average current throug the diode when it conducts.

Let us define I(t) - inductor current averaged over a switching period, $V_g(t)$ - source voltage, V(t) - output voltage (averaged over a switching period). These can be written as I(t) = I + i(t), $V_g(t) = V_g + v_g(t)$, and V(t) = V + v(t) where I, $V_g$ and V are quiescent values and small letters denote perturbations.
Then the FET is on, the voltage across it is $I(t) R_{ON}$. During off time and assuming negligible voltage drop across the rectifying diode, the voltage is equal to the output voltage, V(t). The average (over the switching period) voltage is then $I(t)R_{ON}D(t) + V(t) \cdot (1-D(t))$
We can then write the equation for the diode current as
$$V_g (t) - I(t)R_{ON}D(t) - V(t)\cdot (1-D(t)) = L\frac {dI(t)} {dt}$$
The average (over a switching period) current through the diode is I(t)(1-D(t)) and that gives the second equation:
$$ I(1 - D(t)) = \frac {V(t)} R + C \frac {dV(t)} {dt} $$
Now, you can solve the two equations for the quiescent current that is assuming I, V $V_g$ and D are constant. Then, expand the first equation in the first order of perturbations and you should get the answers you want.

 

[alan123hk]

The home work question state "if your expression contain the quantities Vg or I, you should use the steady state model to eliminate these and express your answers as a functions of above variables only", which including the quiescent duty cycle D, quiescent output voltage V and load resistance R.

This makes me feel a little strange. I personally think it would be better to use Vg instead V to express it, because usually the input voltage Vg is a known parameter and output voltage V is an unknown parameter, especially the voltage conversion ratio becomes complicated when the converter is lossy.

Anyway, according to the second equation shown in #3 as follows

$$ I(1−D(t)) = \frac {V(t)} R + C \frac {dV(t)} {dt} $$

In the steady state, the quiescent current of capacitor is zero, so it can be simplified to $I(1−D)= \frac V R$ where I is quiescent inductor current, D is the quiescent duty cycle, V and R are the quiescent output voltage and load resistance, respectively.

Thus, the quiescent inductor current $I$ is simply equal to $\frac V {(1−D)R}$

Since the quiescent input current $I_{in}$ is equal to the quiescent inductor current $I$ in the boost converter, we can also get the equation $I_{out}=\frac V R =I_{in}(1−D)$