Smoothing/Filtering Data from Analog to Digital Converter

[j777]

Hi,

I am trying to filter noise out of data gathered from an analog to digital converter. I've looked at averaging techniques but I fear that they cause too much data loss. Can anybody recommend other smoothing/filtering techniques that might result in less data loss and can be done dynamically as the data is read?

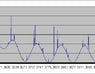
See the attachment to get an idea of what the noise looks like (the sharp spikes throughout the graph).


Thanks

 

[chroot]

Pass it through a digital low-pass filter.

- Warren

 

[j777]

Ok. If that is the best way I'll post further questions about the low-pass filter in the EE forum. Thanks.

 

[chroot]

It's one way -- but it's not necessarily the easiest. Since your signal is very low-frequency (as compared to Nyquist) you could also just find all the samples which are very different from the immediately preceding sample. In other words, find the difference between sample k and sample k-1, and look for large values. These are places where the derivative of the signal is very high -- but since you know the desired signal is slow, you know these points are errors.

Finally, remove any such samples, and replace them with a linear or cubic spline interpolation of the nearby samples.

- Warren

 

[j777]

That sounds like a better idea. I actually tried to implement something like what you have explained but failed to figure out an elegant way to determine if a point was in fact an error. Using the derivative of the signal seems like a good approach. I will give it a try...thank you.