Ran4
- 4
- 0
I'm reading through old exams, but there's not very much in the way of explanation, and this is one of the problems I have that I'm not sure that I fully understand.
We have the material CdTe. What is the highest allowable wavelength that incoming light can have in order to excite an electron from the valence band to the conduction band?
The relevant figure is this one:
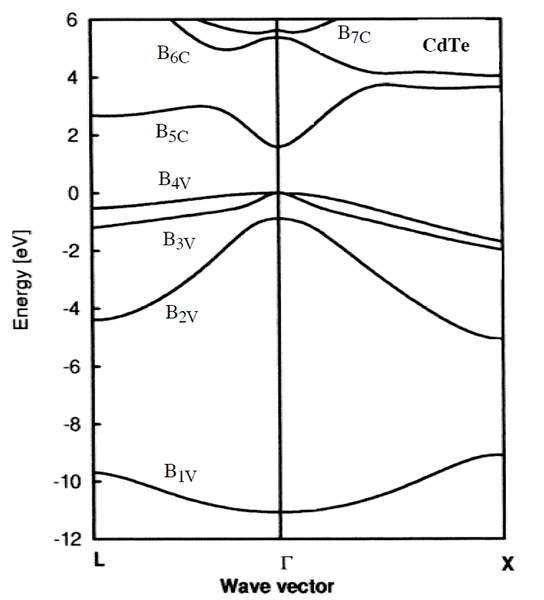
The index V signifies valence electrons, C signifies the conduction band.
The highest wavelength is going to have the lowest energy, so I figure that you want the smallest difference between two energy levels of valence electrons and conduction band electrons. According to the figure that should happen in the [itex]\Gamma[/itex] direction, and if we look at [itex]B_{4V}[/itex] and [itex]B_{5C}[/itex] that would give us about 1.6 eV.
The answer is supposed to be 1.45 eV (which is then used to calculate λ from λ=hc/ε), so I'm not sure if I'm doing this right.
We have the material CdTe. What is the highest allowable wavelength that incoming light can have in order to excite an electron from the valence band to the conduction band?
The relevant figure is this one:
The index V signifies valence electrons, C signifies the conduction band.
The highest wavelength is going to have the lowest energy, so I figure that you want the smallest difference between two energy levels of valence electrons and conduction band electrons. According to the figure that should happen in the [itex]\Gamma[/itex] direction, and if we look at [itex]B_{4V}[/itex] and [itex]B_{5C}[/itex] that would give us about 1.6 eV.
The answer is supposed to be 1.45 eV (which is then used to calculate λ from λ=hc/ε), so I'm not sure if I'm doing this right.