mrshappy0
- 97
- 0
Homework Statement
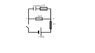
Switch is initially opened with the capacitor uncharged. At t=0 the switch is clsoed. At time=t1 later, the potential difference between A and B is 2.00volts
Find the charge on the capacitor at time t1.
R=10,000ohms
C=2.4nF
Vb=12volts
VA->B-=2.00volts
Homework Equations
I(t)=(V/R)*e^(-t/RC)
q(t)=CV(1-e^(-t/RC))
C=Q/V
The Attempt at a Solution
RC was correctly found to be 40microSeconds.So then the goal is to find the time at t1. The 2volts across A and B must be important to finding t1.
So I assumed that the voltage drop from A-B must be equal to the voltage drop for R3. Thus 2Volt/R=I3.
Then I used I3 to find t1: I3=(V/R)*e^(-t/RC) --> solving for t and then plugging into q(t).
Does this seem right or is my logic wrong?