- #1
14850842
- 4
- 0
Can you please help me solve the equation of motion for the following diagram
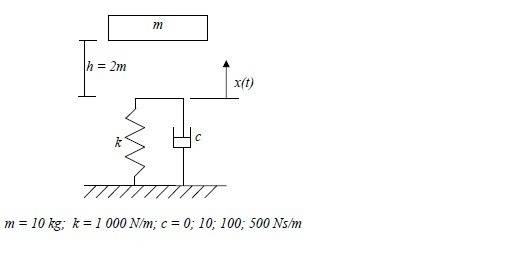
Thanks
Thanks
Solve Equation of Motion for Spring Damper System
Click For Summary
Discussion Overview
The discussion centers around solving the equation of motion for a spring-damper system, specifically focusing on the formulation of the equation based on a provided diagram. The scope includes mathematical reasoning and conceptual clarification related to the dynamics of the system.
Discussion Character
- Exploratory, Technical explanation, Homework-related
Main Points Raised
- One participant requests assistance in solving the equation of motion for a spring-damper system.
- Another participant suggests that the original poster should provide the equation before seeking help.
- A third participant expresses that they only need the equation to proceed with their work.
- A fourth participant provides the equation of motion for the system as m\ddot{x}+c\dot{x}+kx=0, while also indicating uncertainty about the diagram's details.
Areas of Agreement / Disagreement
Participants do not appear to have reached a consensus, as there are differing levels of understanding and clarity regarding the equation and the diagram.
Contextual Notes
There is a lack of clarity regarding the diagram referenced, which may affect the understanding of the system's dynamics. Additionally, the assumptions underlying the equation provided have not been explicitly stated.
- #2
Thaakisfox
- 263
- 0
You should at least write up the equation before asking for help to solve it. So could you write the equation?
- #3
14850842
- 4
- 0
What I need is the equation, the rest I can work from there
- #4
Similar threads
- · Replies 21 ·
- · Replies 16 ·
Automotive
Spring and damper on rocker
- · Replies 2 ·
Engineering
Control System mass spring damper
- · Replies 0 ·
- · Replies 15 ·
- · Replies 1 ·
- · Replies 1 ·
- · Replies 3 ·
- · Replies 9 ·