Solve Gauss' Law Problem: Electric Field at P on Spherical Shell

Click For Summary
SUMMARY

The discussion focuses on solving a Gauss' Law problem involving an insulator shaped as a spherical shell with an inner radius of 4 cm and an outer radius of 6 cm, carrying a total charge of +9 mC. The user attempts to calculate the electric field's y-component at point P, located at (0, -5 cm), using a Gaussian surface of radius 4 cm. The calculation for the enclosed charge, Qin, is incorrectly derived as 7.2e-5, indicating a misunderstanding of the charge distribution within the spherical shell.

PREREQUISITES
  • Understanding of Gauss' Law and its application in electrostatics.
  • Familiarity with spherical coordinates and electric field concepts.
  • Knowledge of charge distribution in insulating materials.
  • Basic calculus for volume calculations of spherical shells.
NEXT STEPS
  • Review the derivation of charge enclosed using Gauss' Law for spherical shells.
  • Learn how to calculate electric fields for different charge distributions, specifically for spherical geometries.
  • Study the concept of electric field lines and their relation to charge distribution.
  • Explore the implications of uniform charge distribution in insulating materials.
USEFUL FOR

Students studying electromagnetism, physics educators, and anyone seeking to deepen their understanding of electric fields and Gauss' Law applications in spherical geometries.

mujadeo
Messages
103
Reaction score
0

Homework Statement



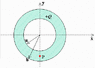
An insulator in the shape of a spherical shell is shown in cross-section above. (see attached .gif) The insulator is defined by an inner radius a = 4 cm and an outer radius b = 6 cm and carries a total charge of Q = + 9 mC (1 mC = 10-6 C). (You may assume that the charge is distributed uniformly throughout the volume of the insulator).

What is Ey, the y-component of the electric field at point P which is located at (x,y) = (0, -5 cm) as shown in the diagram?




Homework Equations


I can't do this I am totally stuck.


The Attempt at a Solution



OK so obviously gauss law.
I chose sphere inside the sphere, of radius 4cm for my gauss surface
i need to calc the charge in this enclosed sphere.

So charge in the sphere should be:

Qin = (r^3 / (R^3 - r^3))*Q

= 7.2e-5

this much is wrong but don't know why
please help --thanks

Heres the drawing on flickr:
http://www.flickr.com/photos/15315161@N02/1607125471/
 

Attachments

  • showme.gif
    showme.gif
    2.8 KB · Views: 584
Last edited:
Physics news on Phys.org
can't see the attachment... but I assume (0, -5cm) is located at a radius of 5cm from the center? If I'm wrong about this let me know.

So using Gauss' law... what is the volume of the insulator enclosed within a radius of 5cm?
 

Similar threads

Gauss' Law: Conductor, Insulator, Electric Field
  • · Replies 7 ·
Replies
7
Views
1K
Gauss' Law applied to this Charged Spherical Shell with a small hole
  • · Replies 10 ·
Replies
10
Views
4K
Electric field at a point inside a non-uniformly charged sphere
  • · Replies 6 ·
Replies
6
Views
2K
Gauss' law problem -- Should the field due to both the inside and outside charges be taken into account?
  • · Replies 28 ·
Replies
28
Views
2K
Electric field external to Conducting Hollow Sphere with charge inside
  • · Replies 23 ·
Replies
23
Views
5K
Using Gauss' Law to find the field at a point
  • · Replies 6 ·
Replies
6
Views
2K
Electrostatics: Gauss' Law Problem Finding the Flux through a Conducting Spherical Shell
  • · Replies 9 ·
Replies
9
Views
2K
I Thought I Understood Gauss' Law (Sheets)
  • · Replies 26 ·
Replies
26
Views
3K
Electric field using Gauss' Law
  • · Replies 3 ·
Replies
3
Views
2K
Question on a Gauss's Law problem
  • · Replies 1 ·
Replies
1
Views
2K