Solve Homework: Find Acceleration & Reaction Force of Wedge

[Bucky]

Homework Statement

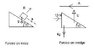
A wedge of mass 4kg and angle 30 degrees is at rest on a smooth horizontal table. a mass of 1kg is placed on the smooth inclined face of the wedge and a horizontal force of 10N is applied to towards the vertical face of the wedge. Show that the acceleration of the wedge is

(40 - root(3g) ) / 17 ~= 1.35m/s.


Also find the reaction force between the wedge and the mass

Homework Equations

The Attempt at a Solution

(from diagrams)

Equation of wedge horizontally

4A = 10 - Rsin30 (1)

Equation of mass horizontally


A + acos30 = Rsin30
A = Rsin30 - acos30 (2)



Equation of mass vertically

asin30 = g - Rcos30 (3)


Substitute (2) into (1)

4(Rsin30 - acos30) = 10 - Rsin30
5Rsin30 - 4acos30 = 10
5Rsin30 = 10 + 4acos30
5R* 1/2 = 4a * root(3)/2 + 10
5R/2 = 2 root(3)a + 10
5R = 4root(3)a + 20
R = ((4root(3)a) / 5) + 4

Now I have 'R' in terms of 'a', but I'm not sure where to go. My notes on this trail off...I seem to substitute R back into equation (1), along with equation (2) but that will just give me R in terms of a again.

 

[enricfemi]

it seems you missed a equation.

you can achieve a=2g-root(3)R from
asin30 = g - Rcos30 (3)

then subtitute it to
5R = 4root(3)a + 20
it can give you R without a

besides, i really cann't understand then method you used in this problem and so as what the A stand for.i suggest you consider more ways.

 

[Bucky]

it seems you missed a equation.

you can achieve a=2g-root(3)R from
asin30 = g - Rcos30 (3)

then subtitute it to
5R = 4root(3)a + 20
it can give you R without a

besides, i really cann't understand then method you used in this problem and so as what the A stand for.i suggest you consider more ways.

where does the 'missing equation' come from?
I can't actually recall why A is there, though I'm sure i need it :/ could it be the force of the mass pushing the wedge back?

 

[enricfemi]

where does the 'missing equation' come from?
I can't actually recall why A is there, though I'm sure i need it :/ could it be the force of the mass pushing the wedge back?

you missed equation (3)

just tell me what the A stand for in the picture in order to let me understand it in your way.

 

[Bucky]

sorry for the delay in replying.

A represents the acceleration of the wedge.

 

[enricfemi]

really sorry for so many days' delay.

in my peasonal sense,non-inertial frame will greatly predigest the problem.just use the wedge as frame.
in addition,you missed a force on wedge in the maps you gave.

happy new day!