alariv8
- 10
- 0
Hydrogen atom: 1/(r^2 )2p state constant problem //1/(r^3) exp. value
Hello, I am new to this forum. I hope it is all right I uploaded problems as image files (in handwriting).
I calculated all (r^(-1), r^(-2) and r^(-3) expectation values for Hydrogen atom for 1s and 2p. Almost all calculations gave the required result - the same as the theoretical formulas with quantum numbers, but r^(-3) for 1s and 2s state give an infinity when calculating using quantum numbers and should give the same when integrating. My question: Why does this integral diverge?
The first problem:
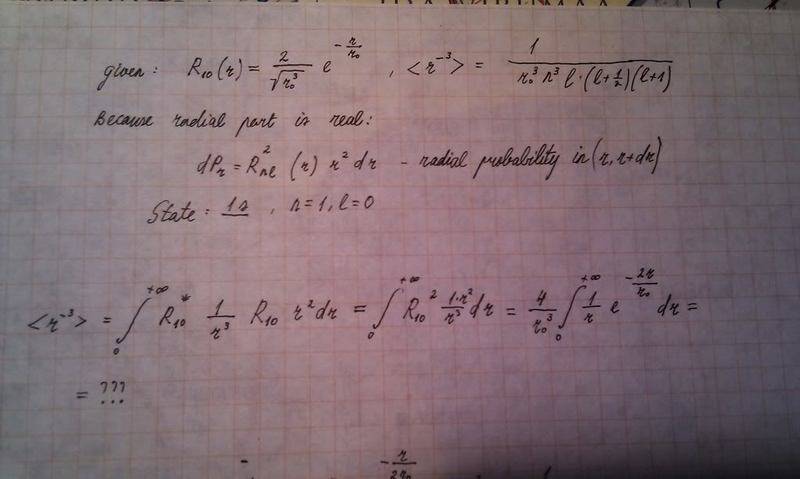
I found out that there is a similar formula on integral-table.com
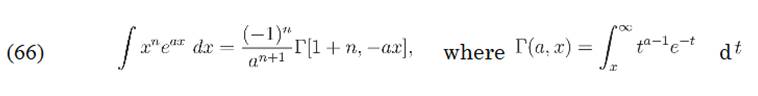
but I guess there n is a natural number, am I right?
r^(-2) for 2p - there I have a constant problem:
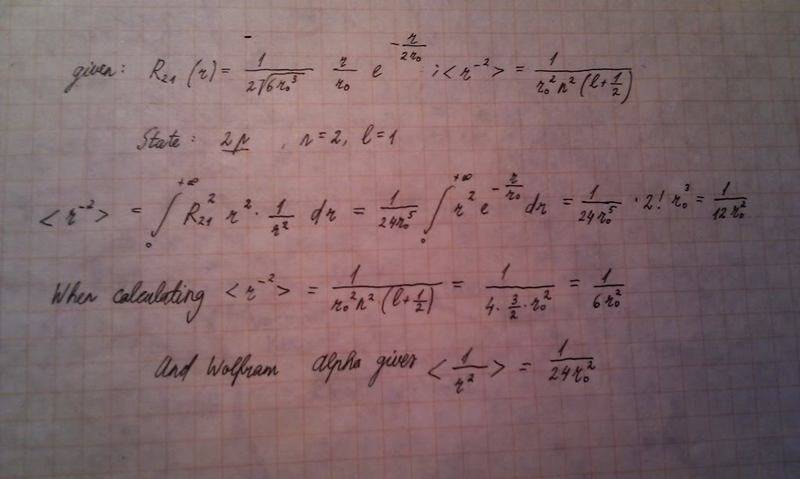
Homework Statement
Hello, I am new to this forum. I hope it is all right I uploaded problems as image files (in handwriting).
I calculated all (r^(-1), r^(-2) and r^(-3) expectation values for Hydrogen atom for 1s and 2p. Almost all calculations gave the required result - the same as the theoretical formulas with quantum numbers, but r^(-3) for 1s and 2s state give an infinity when calculating using quantum numbers and should give the same when integrating. My question: Why does this integral diverge?
The first problem:
I found out that there is a similar formula on integral-table.com
but I guess there n is a natural number, am I right?
The Attempt at a Solution
Homework Statement
r^(-2) for 2p - there I have a constant problem:
Homework Equations
The Attempt at a Solution
Last edited: