emrock
- 2
- 0
- TL;DR Summary
- Looking for context around an equation
I am hoping that people here might be able to provide insight into
what context/s this equation might be relevant, particularly the contents of the brackets.
I am aware it is a strange request, related to puzzle solving,
but perhaps someone can help guide me in an interesting direction.
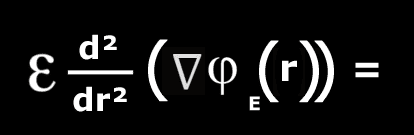
what context/s this equation might be relevant, particularly the contents of the brackets.
I am aware it is a strange request, related to puzzle solving,
but perhaps someone can help guide me in an interesting direction.
