Solve Normal Stress Problem: Width of 30kN Offset Link, 73MPa Max

ashleyw6
Messages
3
Reaction score
0

Homework Statement



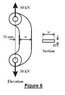
An offset link supports a load of 30 kN as shown in figure 6. Determine its required width w if the total (combined) normal stress is not to exceed 73 MPa?

The cross section of the link is rectangular and has thickness of 40 mm

Homework Equations



stress= N/A

I have tried many different ways to solve this problem but end up hitting a wall! any help would be greatly appreciated :)
 

Attachments

  • Figure 6.JPG
    Figure 6.JPG
    3.5 KB · Views: 372
Last edited:
Physics news on Phys.org
hi ashley, welcome to pf

can't see the pic yet, they usually take a while to claar, what have you tried?
 
Hi lanedance,

I have tried using the shearforce formula: \tau=VQ/It but am unable to get any where...
 
without being able to see the pic... why are you finding shear stress? when you want to find normal stress (Force/Area)
 
wow how dumb do i look :P i have tried solving the question in every way i could think of but i am doing something wrong. I have used the normal shear formula but again to no avail.
Thanks for the help!
 

Thread 'Direction of the magnetic field of an oscillating charge'

Hello everyone, I’m considering a point charge q that oscillates harmonically about the origin along the z-axis, e.g. $$z_{q}(t)= A\sin(wt)$$ In a strongly simplified / quasi-instantaneous approximation I ignore retardation and take the electric field at the position ##r=(x,y,z)## simply to be the “Coulomb field at the charge’s instantaneous position”: $$E(r,t)=\frac{q}{4\pi\varepsilon_{0}}\frac{r-r_{q}(t)}{||r-r_{q}(t)||^{3}}$$ with $$r_{q}(t)=(0,0,z_{q}(t))$$ (I’m aware this isn’t...
View full post »

Thread 'Initial conditions for orbits around a wormhole'

Hi, I had an exam and I completely messed up a problem. Especially one part which was necessary for the rest of the problem. Basically, I have a wormhole metric: $$(ds)^2 = -(dt)^2 + (dr)^2 + (r^2 + b^2)( (d\theta)^2 + sin^2 \theta (d\phi)^2 )$$ Where ##b=1## with an orbit only in the equatorial plane. We also know from the question that the orbit must satisfy this relationship: $$\varepsilon = \frac{1}{2} (\frac{dr}{d\tau})^2 + V_{eff}(r)$$ Ultimately, I was tasked to find the initial...
View full post »

Similar threads

Calculating Chain Link Strength: Which Method Should You Use?
Replies
7
Views
4K
Box Beam stress problem with welding
Replies
16
Views
2K
Wind-Induced Bending Stress on Chimney with Rectangular Cross-Section
Replies
2
Views
2K
Calculate the maximum vertical point force P that this beam can sustain
Replies
1
Views
2K
Normal Stress: Compression vs Tension
Replies
8
Views
8K
Finding the Force P from Normal Stress
Replies
3
Views
6K
Strength of Materials Stress Question
Replies
8
Views
2K
Structural Mechanics. bending moment and bending stress
Replies
17
Views
5K
How Do You Calculate the Maximum Average Normal Stress in Link BD?
Replies
2
Views
4K
Max value of the average normal stress in the links.
Replies
1
Views
3K

Hot Threads

Recent Insights

Back
Top