Solve Rigid Body Motion: Pendulum Rod & Disk Eqns of Motion

[Logarythmic]

Problem statement:
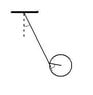
Consider a pendulum consisting of two parts: a uniform rod of mass m, length l, negligible thickness and with one end fixed; and a uniform disk of mass \mu and radius \rho.
The rod is moving in a plane, and the disk is attached at a point P on its boundary to the non-fixed end of the rod, in such a way that it can freely rotate about P in the plane in which the rod is moving.
Obtain the Lagrangian and the equations of motion.


I suppose I should divide this into two parts; one for the rod and one for the disk.
For the rod I get

T_1 = \frac{1}{2} I_1 \dot{\theta}_1^2 + \frac{1}{2} m(\dot{x}_1^2 + \dot{y}_1^2)

,where the index 1 is the rod, and

V_1 = mgh = mg \frac{l}{2} (1 - \cos \theta_1).

The moment of inertia for the rod is

I_1 = \frac{1}{3} m l^2.

So far so good, I think.. But how should I do with the disc? Should I treat this the same way and just use a superposition of the two lagrangians? And how do I get the moment of inertia?

 

[dextercioby]

Can you post a picture ? I'm unable to imagine the setup.

Daniel.

P.S. There's no such thing as a superposition of lagrangians.

 

[Logarythmic]

This is what I think it should look like. I guess it's like a double pendulum with two rigid bodies.

 

[OlderDan]

This is what I think it should look like. I guess it's like a double pendulum with two rigid bodies.

The double pendulum sounds right to me. The moment of inertia of the disk about its pivot point P can be obtained using the parallel axis theorem. I think you would want to use two angles as your generalized coordinates, one for the rod and one for the disk.

 

[Logarythmic]

So the kinetic energies are just

T_{rod} = \frac{1}{2} I_O \dot{\theta}_1^2

and

T_{disc} = \frac{1}{2} I_P \dot{\theta}_2^2

or should I include translation movement aswell?

 

[Logarythmic]

I get the equations of motion to be

0 = \mu \left[ l \ddot{\theta}_1 + R \dot{\theta}_2 \sin{(\theta_1 - \theta_2)} (\dot{\theta}_1 - \dot{\theta}_2 + \dot{\theta}_1 \dot{\theta}_2) + R \ddot{\theta}_2 \cos{(\theta_1 - \theta_2)} + g \sin{\theta_1} \right] + \frac{1}{2} mg \dot{\theta}_1 \sin{\theta_1}

and

0 = R \ddot{\theta}_2 + l \ddot{\theta}_1 \cos{(\theta_1 - \theta_2)} - l \dot{\theta}_1^2 \sin{(\theta_1 - \theta_2)} + g \sin{\theta_2}

where I have used R instead of \rho
Could this be correct?

 

[OlderDan]

So the kinetic energies are just

T_{rod} = \frac{1}{2} I_O \dot{\theta}_1^2

and

T_{disc} = \frac{1}{2} I_P \dot{\theta}_2^2

or should I include translation movement aswell?

You will need translation and rotation for the disk- translation of the CM and rotation about the CM. I did not look at your equations of motion yet. Did you include more than what you have here?

 

[Logarythmic]

Yes I used

T_{rod} = \frac{1}{2} I_O \dot{\theta}_1^2

and

T_{disc} = \frac{1}{2} I_P \dot{\theta}_2^2 + \frac{1}{2} m (\dot{x}_2^2 + \dot{y}_2^2)

where I_O is the moment of inertia about the upper end of the rod, I_P is the moment of inertia about the pivot point P and x_2 and y_2 are the coordinates of the c.m. of the disc.

 

[OlderDan]

Yes I used

T_{rod} = \frac{1}{2} I_O \dot{\theta}_1^2

and

T_{disc} = \frac{1}{2} I_P \dot{\theta}_2^2 + \frac{1}{2} m (\dot{x}_2^2 + \dot{y}_2^2)

where I_O is the moment of inertia about the upper end of the rod, I_P is the moment of inertia about the pivot point P and x_2 and y_2 are the coordinates of the c.m. of the disc.

With x and y the coordinates of the CM, then the I for the disc should be the I about the center of mass.

 

[Logarythmic]

But if I'm using I about P, what should I include then?

 

[OlderDan]

But if I'm using I about P, what should I include then?

You could express the moment of inertia about the center of mass in terms of the moment of inertia about P by using the parallel axis theorem, but why would you want to? The CM is a special point in an assembly of particles or a rigid body that (among other things) permits the separation of kinetic energy into the translation of the CM term and the rotation about the CM term. No arbitrary point is so well behaved.

When you used x and y translational velocities for part of the kinetic energy, you were already including some of the energy of rotation about P. If you use I about point P, you will be couble counting some of the energy contribution.

 

[Logarythmic]

So

T_{rod} = \frac{1}{2} I_O \dot{\theta}_1^2
and
T_{disc} = \frac{1}{2} I_{CM} \dot{\theta}_2^2 + \frac{1}{2} m (\dot{x}_2^2 + \dot{y}_2^2)

is correct?

 

[OlderDan]

So

T_{rod} = \frac{1}{2} I_O \dot{\theta}_1^2
and
T_{disc} = \frac{1}{2} I_{CM} \dot{\theta}_2^2 + \frac{1}{2} m (\dot{x}_2^2 + \dot{y}_2^2)

is correct?

Looks right to me. With Io being the moment of inertial of the rod about its end.

For what it's worth, I found it easier to do the algebra using the angle between the radius from P to the disk center and the vertical. That would be the sum of your angles I believe. When the algebra is done it can be expressed in terms of your angles.

 

[Logarythmic]

That's how I've done it. =) Thanks for your help!

 

[epdu]

which one is right?
Could you explain a little?

That's how I've done it. =) Thanks for your help!