ataglance05
- 43
- 0
ROTATIONAL MOTION not circular; sorry
A wheel 1 meter in diameter (radius 0.5 m) is rotating at 100 revolutions per minute without slipping along a level stretch of road and passes mile marker 0 at 12:00 noon. It contunes past mile marker 0 for 10 minutes and then has a period of angular acceleration of 2.5*10^-2 radians per second^2 for a period of 90 seconds. After the 90 sec acceleration period, the wheel rolls on for 1 hour. At the end of the hour the wheel undergoes a deceleration of 1.5*10^-2 radians per sec^2 until it stops.
How far is the wheel in km from mile marker 0? What time is it when it stops?
I believe...
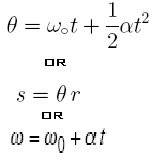
What I'm trying to do is get the distance for each time the acceleration changes.
So, below is how far it went in 10 minutes before its acceleration of 2.5810^-2 radians/sec^2:
100 revs=200(pi) radians/60sec * 600sec=
=10.47 * 600sec
=6.283*10^3 rads/10 min
S=(theta)(r)
S=(6.283*10^3 rads/10 min)(0.5m)
S=3141.5927 m or 3.1459 km
I have no clue what to do after that. I think I should continue on with trying to get the distance it went when it accelerates for 90 seconds, but I have no clue how to implement that acceleration to affect the distance travelled?
Please help! Thank you!
Homework Statement
A wheel 1 meter in diameter (radius 0.5 m) is rotating at 100 revolutions per minute without slipping along a level stretch of road and passes mile marker 0 at 12:00 noon. It contunes past mile marker 0 for 10 minutes and then has a period of angular acceleration of 2.5*10^-2 radians per second^2 for a period of 90 seconds. After the 90 sec acceleration period, the wheel rolls on for 1 hour. At the end of the hour the wheel undergoes a deceleration of 1.5*10^-2 radians per sec^2 until it stops.
How far is the wheel in km from mile marker 0? What time is it when it stops?
Homework Equations
I believe...
The Attempt at a Solution
What I'm trying to do is get the distance for each time the acceleration changes.
So, below is how far it went in 10 minutes before its acceleration of 2.5810^-2 radians/sec^2:
100 revs=200(pi) radians/60sec * 600sec=
=10.47 * 600sec
=6.283*10^3 rads/10 min
S=(theta)(r)
S=(6.283*10^3 rads/10 min)(0.5m)
S=3141.5927 m or 3.1459 km
I have no clue what to do after that. I think I should continue on with trying to get the distance it went when it accelerates for 90 seconds, but I have no clue how to implement that acceleration to affect the distance travelled?
Please help! Thank you!
Last edited: