ace214
- 28
- 0
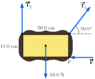
A uniform 10.0-N picture frame is supported as shown in Figure P8.62. Find the tension in the cords and the magnitude of the horizontal force at P that are required to hold the frame in the position shown.

T = Fxsintheta
So I got what's going on in each direction in a separate equation but I need another equation for the third unknown...
T1sin50 = T2
T1cos50 = F
What am I missing?
ADD: Just to fill in, the whole equations have the distances but if you use the point of gravity as your axis in each case, they are all equidistant from the axis so the distances cancel out, and the torque due to the weight of the picture ends up being 10N(0m) = 0 N*m
T = Fxsintheta
So I got what's going on in each direction in a separate equation but I need another equation for the third unknown...
T1sin50 = T2
T1cos50 = F
What am I missing?
ADD: Just to fill in, the whole equations have the distances but if you use the point of gravity as your axis in each case, they are all equidistant from the axis so the distances cancel out, and the torque due to the weight of the picture ends up being 10N(0m) = 0 N*m
Attachments
Last edited: