rum2563
- 89
- 1
Homework Statement
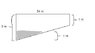
A swimming pool is 24 m long by 8 m wide, 1 m deep at the shallow end and 3 m deep at the deep end, the bottom being an inclined plane. If water is pumped into the empty pool at a rate of 2m^3/min, then how fast is the water level rising at the moment when the water is 1 m deep at the end of the pool.
Homework Equations
dh/dt = 1/As x dV/dt
As: area of exposed surface
The Attempt at a Solution
Basically I used ratios to get the length of the pool when the height is 1 m deep.
1/3 = x/24
So x = 8 m.
Then As = 8*8 = 64 m^2
dh/dt = 2/64
= 1/32 m/min
I am not sure what I am doing wrong. I have my diagram attached. Please tell me what I am doing wrong. Also, if you have the answer please tell me because I need this urgently. I can use the answer and then work it back to get everything right.
Thanks.