Solve Weird Matrix Equation to Get Values for P

[maistral]

So while I was trying to browse some notes with regard to Laplace transforms in solving systems of ODE, this matrix came up:

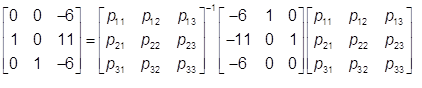
I could easily just use RK4 and call it a day to nuke the systems of ODE, but this actually made me curious. Apparently one can transform the matrix DE into another form, then this appeared.

How do I get the values for P?

 

[S.G. Janssens]

I don't think such $P$ exists. The numerical matrices on the left and right have different eigenvalues.

 

[DrClaude]

I don't think such $P$ exists. The numerical matrices on the left and right have different eigenvalues.

It exists and is not unique.

I was able to obtain a possible $P$ using Mathematica. However, I do not know how to do it in a rigorous fashion.

 

[S.G. Janssens]

What do you find for the eigenvalues of the left and right numerical matrices? For the one on the left I get one real eigenvalue and a complex-conjugate pair, while for the matrix on the right I get $\{-3,-2,-1\}$. So these two matrices cannot be similar.

(If such $P$ would exist, it would not be unique indeed, because every nonzero multiple of $P$ would also qualify.)

 

[DrClaude]

What do you find for the eigenvalues of the left and right numerical matrices? For the one on the left I get one real eigenvalue and a complex-conjugate pair, while for the matrix on the right I get $\{-3,-2,-1\}$. So these two matrices cannot be similar.

I made a mistake and used +11 instead of -11 in the right matrix. My guess is that there is an error in the OP and that the two matrices differ only by the arrangement of the numerical values.

 

[StoneTemplePython]

assuming the stated typo, consider using the reflection matrix

$\mathbf J = \left[\begin{matrix}0 & 0 & 1\\0 & 1 & 0\\1 & 0 & 0\end{matrix}\right]$

which is a permutation matrix (and involutary)

note:
For the nice case of diagonalizable matrices with the same spectrum (and in particular the extra nice case where all eigenvalues are distinct), the general approach is
$\mathbf S^{-1} \mathbf A \mathbf S= \mathbf D$
and
$\mathbf U^{-1} \mathbf B \mathbf U= \mathbf D$

so
$\mathbf U^{-1} \mathbf B \mathbf U= \mathbf S^{-1} \mathbf A \mathbf S$
$\mathbf B = \mathbf U\mathbf S^{-1} \mathbf A \mathbf S\mathbf U^{-1}$
setting $\mathbf P:= \mathbf S\mathbf U^{-1}$
gives
$\mathbf B = \mathbf P^{-1} \mathbf A \mathbf P$

the fact that the eigenvalues are distinct proves that $\mathbf P$ is unique (up to rescaling)

but in this case I could just eyeball the problem as a graph isomorphism and come up with $\mathbf J$