trekie4ever
- 3
- 0
[SOLVED] Hydrostatic Forces
Any Help would be GREATLY appreciated. My grade depends on me understanding this.
A tank contains freshwater. The end of a tank containing water is vertical and has the indicated shape. Explain how to approximate the hydrostatic force against the end of the tank by a Riemann sum. Then express the force as an integral and evaluate it.
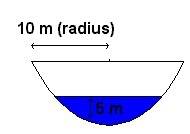
F=pgAd
A=wdx
F= int 0->5 1000(9.8)2sqrt(100-y^2)(5)
98000*int 0->5 sqrt(100-y^2)
u=100-y^2
-1/2*du=dy
98000*int 75->100 u^(.5)
98000{(2/3)u^(3/2)} 75->100
64171414.85 N
Any Help would be GREATLY appreciated. My grade depends on me understanding this.
Homework Statement
A tank contains freshwater. The end of a tank containing water is vertical and has the indicated shape. Explain how to approximate the hydrostatic force against the end of the tank by a Riemann sum. Then express the force as an integral and evaluate it.
Homework Equations
F=pgAd
A=wdx
The Attempt at a Solution
F= int 0->5 1000(9.8)2sqrt(100-y^2)(5)
98000*int 0->5 sqrt(100-y^2)
u=100-y^2
-1/2*du=dy
98000*int 75->100 u^(.5)
98000{(2/3)u^(3/2)} 75->100
64171414.85 N
Last edited: