Solving a 'skew' quadrilateral for vertex position.

[athuss]

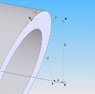
I've been scratching my head over this one. I'm trying to find a system of equations to solve for points R and S. The known parameters are: Point Q, tangent vector t and the axis vector a.

The following vectors are perpendicular to each other:
a,d
a,b
b,c
c,t
d,t

The other known parameter is that vector c has a magnitude of 0.0625. This creates a quadrilateral that is skew, with vector c and a being at an angle to each other and pulling the sides out of plane.

I'm trying to find the mathematical way of solving this across a number of points. SolidWorks can find one valid answer for the sample (and fully defines the topology) but I cannot get a system of equations to solve to match in Mathcad.

Any method would be appreciated? I'm trying to get it so that I don't have to rely on the SolidWorks sketch engine to reduce computation times.

 

[chiro]

Hey athuss and welcome to the forums.

So looking at your diagram, here is what we know:

Q + c = R
R + b = S
T + a = S
Q + d = T

t^unit x c^unit = d^unit

The approach I am going to take is to use the tangent vector to get the plane that contains the points Q, R, and T as well as the vectors c and d.

We know the plane equation since we have a point on the plane Q and our normal vector t. If we use n to be the normalized vector for t we get our plane equation to be n . (r - Q) = 0.

Now from this point we need to establish how the direction of a affects the direction of either c or d directly.

Now we know that a and c are parallel since a,b orthogonal and b,c orthogonal which means a^hat = c^hat. But because we know this, it means that we can calculate d^hat by calculating d^hat = t^hat x c^hat where the hat vectors are normalized.

Now we have the vector c since we have its magnitude so we get c = c^hat*||c||.

From this we have R by using R = Q + c. So that's R down.

Please tell if I've screwed up anywhere with regards to assumptions.

 

[athuss]

Hello chiro, thanks for the help.

I worked through your reply and I think that there is one assumption that isn't true. That is:

t^unit x c^unit = d^unit

t^unit and c^unit are perpendicular, as are t^unit and d^unit, but c^unit and d^unit are not.

This means that a and c are not parallel and the vector c is still unknown.

I've attached another view to show the skew of the quadrilateral. I think there is enough information to solve this but I haven't yet found it.

 

[chiro]

Thanks for that athuss! I'll take a look later though it's getting a little late here.