Coop
- 40
- 0
Hi,
I am working on this water pressure problem,
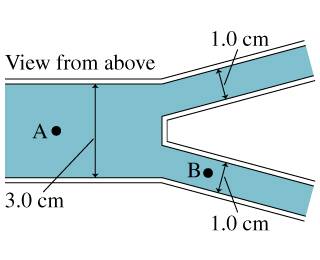
given:
v_A = 2.0 \frac{m}{s}
gauge pressure_A = 50 kPa
the view is from above, no height changes
find: gauge pressure @ B
so,
A_Av_A=2(A_Bv_B)
1.5*10^{-2}m^2(2.0\frac{m}{s})=2(5*10^{-3}m^2v_B)
v_B=9.0\frac{m}{s}
Bernoulli's equation (w/o the \rho gh components bc height is constant):
p_A+\frac{1}{2}\rho _Av_A^2=p_B+\frac{1}{2}\rho _Bv_B^2
My question is, how come the right side of the equation is not 2(p_B+\frac{1}{2}\rho _Bv_B^2)? Shouldn't there be a coefficient of two, because the pipe splits in half?
Thanks
I am working on this water pressure problem,
given:
v_A = 2.0 \frac{m}{s}
gauge pressure_A = 50 kPa
the view is from above, no height changes
find: gauge pressure @ B
so,
A_Av_A=2(A_Bv_B)
1.5*10^{-2}m^2(2.0\frac{m}{s})=2(5*10^{-3}m^2v_B)
v_B=9.0\frac{m}{s}
Bernoulli's equation (w/o the \rho gh components bc height is constant):
p_A+\frac{1}{2}\rho _Av_A^2=p_B+\frac{1}{2}\rho _Bv_B^2
My question is, how come the right side of the equation is not 2(p_B+\frac{1}{2}\rho _Bv_B^2)? Shouldn't there be a coefficient of two, because the pipe splits in half?
Thanks