- #1
Paiwand
- 9
- 0
Hi all,
I am currently self teaching physics and have come across something i don't know how to do.
There are 2 cars, Cars 1 and 2, traveling at a velocity of 60km/h (16.67m/s) in the eastern direction with a gap of 5 metres between each other. Car 2 is in front of Car 1. Car 2 decelerates to 50km/h (13.89m/s) over 1 second (deceleration of roughly 2.78m/s^2). Car 1 knows that since it is going 2.78m/s faster it will close the 5m gap in roughly 1.8 seconds, so it steers north to avoid collision (assume it does not/cannot brake). Hence, Car 1 makes a partial impact with the rear of Car 2 as it is steering north. Out of the 1.8m rear car width of Car 2, Car 1 makes impact with 40cm of it.
My question is how does this 40cm impact affect the velocity in the eastern direction of Car 1?
Here are some more values I have.
Both the cars weigh 1820kg (same car).
Rolling friction of 0.43m/s^2, (779.27 N)
Have not come up with a steering force yet, if it is relevant just assume a value.
Here is a diagram.
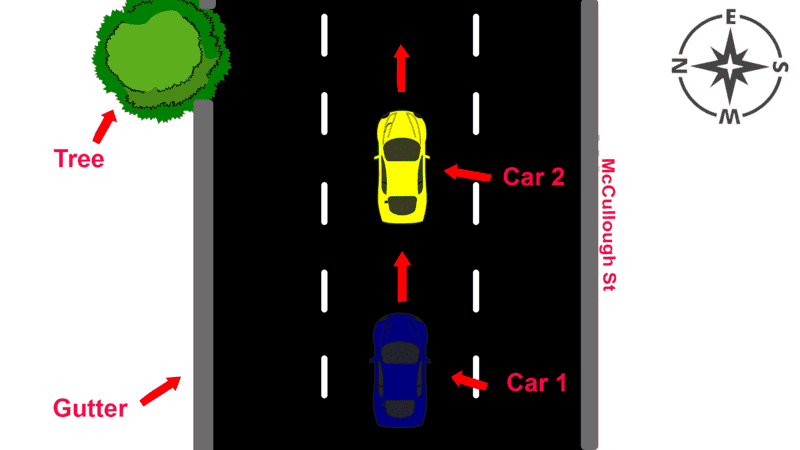
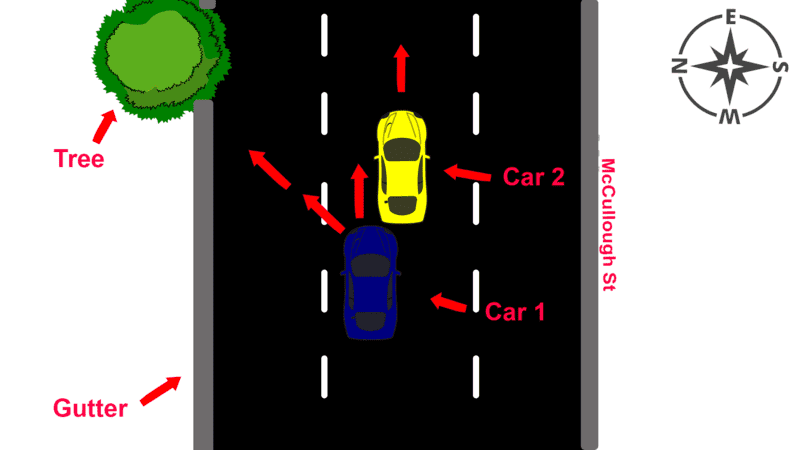
Furthermore, if anymore values are required to solve for this, just assume them. (Most of these numbers are made up by myself as the only stimulus I was given is a police report based on the incident.)
And ignore the other features of the images i have uploaded, they are for the rest of the scenario.
Thanks all :)
I am currently self teaching physics and have come across something i don't know how to do.
There are 2 cars, Cars 1 and 2, traveling at a velocity of 60km/h (16.67m/s) in the eastern direction with a gap of 5 metres between each other. Car 2 is in front of Car 1. Car 2 decelerates to 50km/h (13.89m/s) over 1 second (deceleration of roughly 2.78m/s^2). Car 1 knows that since it is going 2.78m/s faster it will close the 5m gap in roughly 1.8 seconds, so it steers north to avoid collision (assume it does not/cannot brake). Hence, Car 1 makes a partial impact with the rear of Car 2 as it is steering north. Out of the 1.8m rear car width of Car 2, Car 1 makes impact with 40cm of it.
My question is how does this 40cm impact affect the velocity in the eastern direction of Car 1?
Here are some more values I have.
Both the cars weigh 1820kg (same car).
Rolling friction of 0.43m/s^2, (779.27 N)
Have not come up with a steering force yet, if it is relevant just assume a value.
Here is a diagram.
Furthermore, if anymore values are required to solve for this, just assume them. (Most of these numbers are made up by myself as the only stimulus I was given is a police report based on the incident.)
And ignore the other features of the images i have uploaded, they are for the rest of the scenario.
Thanks all :)