masterjoda
- 21
- 0
Homework Statement
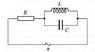
Find the current in them in this circuit, if we know R=X_L, X_C and u=5sin(314t)
The Attempt at a Solution
First , 5=U_0, 314=\omega and voltage we can write as u=U_0cos(\omega t + \frac{\pi}{2}) and u=U_0 e^{i\frac{\pi}{2}}=iU_0. U is the voltage at the source U_1 in the branch and U_2 at the resistor. Now U=U_1+U_2 or U=IR+IZ where \frac{1}{Z}=\frac{1}{iL\omega}-\frac{C\omega}{i} or Z=\frac{iL\omega}{1-CL\omega^2}
Now the current is I=\frac{U}{R+Z} or when it is arranged I=\frac{iU_0(1-CL\omega^2)}{iL\omega (2-CL\omega^2)}. Now I don't know how to complete the calculation to reduce it to the form like this I_0sin(\omega t + \theta).