physpopib
- 1
- 0
Been stumped on these 2 questions for at least a week.
Both diagrams scanned + uploaded.
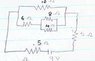
23.Find the current in the 8 ohm resistor.
1/Req1=1/8+1/4
2.67+6=8.67
1/Req2=1/8.67+1/10
R=4.27+.5+5=10.14
I first found the voltage drop in each resistor.
I=V/R
I=9/10.14=.89A
volt.drop .5 resistor=.5*.89=.445V
volt.drop 5 resistor=5*.89=4.45V
volt.drop 4.27 resistor=4.27*.89=3.8V
Then I solved for current in the 8 ohm resistor.
I=[9V-(.89A)*(.5*5)]/x ohm
And that's where I'm stuck. Don't know what ohm to divide by. I think 25 but I don't know why.
35.What would current I1 be if the 12 ohm resistor were shorted out(r=1 ohm)?
OK...this is where I'm just screwed by Kirchhoff's Laws.
I'm thinking:
I3=I2+I1
Loop 1: 12=(1)I1+(8)I2
Loop 2: 12=(1)I2+(10)I2+(12)I2
Loop 3: 6=(1)I3+(18)I3+(15)I3+(10)I2+(1)I2
 Completely stuck. Help please.
Completely stuck. Help please.
Both diagrams scanned + uploaded.
23.Find the current in the 8 ohm resistor.
1/Req1=1/8+1/4
2.67+6=8.67
1/Req2=1/8.67+1/10
R=4.27+.5+5=10.14
I first found the voltage drop in each resistor.
I=V/R
I=9/10.14=.89A
volt.drop .5 resistor=.5*.89=.445V
volt.drop 5 resistor=5*.89=4.45V
volt.drop 4.27 resistor=4.27*.89=3.8V
Then I solved for current in the 8 ohm resistor.
I=[9V-(.89A)*(.5*5)]/x ohm
And that's where I'm stuck. Don't know what ohm to divide by. I think 25 but I don't know why.
35.What would current I1 be if the 12 ohm resistor were shorted out(r=1 ohm)?
OK...this is where I'm just screwed by Kirchhoff's Laws.
I'm thinking:
I3=I2+I1
Loop 1: 12=(1)I1+(8)I2
Loop 2: 12=(1)I2+(10)I2+(12)I2
Loop 3: 6=(1)I3+(18)I3+(15)I3+(10)I2+(1)I2