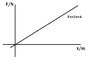
The discussion focuses on solving energy-related problems involving work and potential energy. Participants analyze the calculation of work done using the force function F(x) = 2x + 4 and confirm that the method of integrating W = ∫Fdx is valid. The concept of cosθ is clarified as the angle between the force and displacement vectors, emphasizing the importance of identifying their directions. A key point raised is that the change in potential energy is non-zero due to the force being a function of x, contrasting with scenarios where forces are constant. The conversation underscores the relationship between work, potential energy, and the angles involved in these calculations.