Solving for Forces in a Uniform Field: A Circuit Analysis

[radicaled]

Homework Statement

the current is i, the circuit is in a uniform magnetic field B normal to the plane of the circuit as indicated
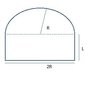
Attached is the circuit

Homework Equations

Get the forces acting on each of their sides. Direction and data module for the following:
L = 10cm
R = 10cm
I = 5A
B = 3.4mT

The Attempt at a Solution

The force for the semi circunference is easy F=I.l.B = IπRB
But I don't agree with a teammate, about the rest.
The bottom of the rectangle should be F=IlB = I2RB
The sides of the rectangle oppose each other so the force should be 0?

 

[TSny]

Hi, Radicaled

The Attempt at a Solution

The force for the semi circunference is easy F=I.l.B = IπRB

It's not quite that easy Don't forget that the force on each infinitesimal section of current is a vector (with direction!). So, it's a vector addition problem.

The bottom of the rectangle should be F=IlB = I2RB
The sides of the rectangle oppose each other so the force should be 0?

ok with the bottom, except you should probably include the direction of the force. For the two vertical sides, the problem seems to want you to state the force on each side separately.

 

[radicaled]

Ok, so I did this:
For the semi circumference
F = I \bar{I}x\bar{B} in the -j direction
So F = 5A \pi0.1m 3.4x10^{-3}T = 5.3x10^{-3}N

Now for the sides of the rectangle:
F = I \bar{I}x\bar{B} in the -i and in +i direction. So they cancel each other?
F = 5A 0.1m 3.4x10^{-3}T = 1.7x10^{-3}N

The base of the rectangle should be like this
F = I \bar{I}x\bar{B} in the -j direction
F = 5A 2x0.1m 3.4x10^{-3}T = 3.4x10^{-3}N

If the sides of the rectangle are 0, I would be able to sum only the base of the rectangle and the semi circumference.
So the total force should be F = 3.4x10^{-3}N + 5.3x10^{-3}N

 

[TSny]

Ok, so I did this:
For the semi circumference
F = I \bar{I}x\bar{B} in the -j direction
So F = 5A \pi0.1m 3.4x10^{-3}T = 5.3x10^{-3}N

You haven't yet taken into account the vector nature of the force on each infinitesimal section of the semicircle. What would be the direction of the force on a small section of the semicircle at the far left side where the section is essentially vertical? What would be the direction of the force on a section at the far right side of the semicircle? How about for a section at the top of the semicircle? Think about some other sections. (It would help if you would indicate which direction you are choosing for the current in the circuit and which direction you are choosing for B.)

Now for the sides of the rectangle:
F = I \bar{I}x\bar{B} in the -i and in +i direction. So they cancel each other?
F = 5A 0.1m 3.4x10^{-3}T = 1.7x10^{-3}N

That looks good.

The base of the rectangle should be like this
F = I \bar{I}x\bar{B} in the -j direction
F = 5A 2x0.1m 3.4x10^{-3}T = 3.4x10^{-3}N

OK, but is the direction of the force on the bottom going to be the same direction as the force on the semicircle?

 

[radicaled]

Sorry i think I forgot to add that.
The direction of the current I took was clockwise.
The magnetic field, comes from the exercise description, is perpendicular to the plane of the circuit.

 

[TSny]

Sorry i think I forgot to add that.
The direction of the current I took was clockwise.
The magnetic field, comes from the exercise description, is perpendicular to the plane of the circuit.

Ok, good. But you'll still need to choose B either "out of the page" or "into the page".

 

[radicaled]

We consider the B into the page

 

[TSny]

We consider the B into the page

OK, then the direction of the force on the bottom side of the loop is -j as you stated. Good.

So, the only thing left is to get the correct force on the semicircle. The usual way to do this is by integration of the force over all the infinitesimal length elements of the semicircle.