Solving for Sin with no calculator

  • Context: High School 
  • Thread starter Thread starter BeautifulLight
  • Start date Start date
  • Tags Tags
    Calculator Sin
Click For Summary

Discussion Overview

The discussion revolves around solving for the sine of an angle without the use of a calculator, specifically addressing the calculation of sinθ given as 5/3, which leads to confusion regarding its validity and the corresponding angle. Participants explore methods of approximation and the implications of sine values exceeding 1.

Discussion Character

  • Homework-related
  • Technical explanation
  • Debate/contested

Main Points Raised

  • One participant states sinθ = 5/3 and calculates it as 1.6, expressing a desire to convert this to an angle of 35.87°.
  • Another participant points out the need for a calculator or sine table to find the angle corresponding to sinθ = 3/5 = 0.6.
  • A participant raises the issue of preparing for an exam where calculators are not allowed, questioning the feasibility of finding the angle without one.
  • One participant critiques the misuse of the sine formula, noting that sine values must be between -1 and +1, indicating that a value larger than 1 is incorrect.
  • Some participants suggest the relevance of memorizing angles associated with Pythagorean triples, such as those in a 3-4-5 triangle, as a potential method for recalling sine values.
  • Another participant mentions that common angles to memorize include 0°, 30°, 45°, 60°, and 90°, along with their counterparts in other quadrants, but notes that these are not typically derived from Pythagorean triples.

Areas of Agreement / Disagreement

Participants express disagreement regarding the validity of the sine value calculated as 5/3, with some emphasizing the impossibility of finding such a sine value without a calculator or table. There is no consensus on how to approach the problem effectively without these tools.

Contextual Notes

Participants highlight limitations in the original calculation, including the incorrect application of the sine formula and the implications of exceeding the sine value range. The discussion does not resolve these issues.

Who May Find This Useful

This discussion may be useful for students preparing for exams that prohibit calculators, as well as those interested in understanding the limitations of trigonometric calculations and the importance of memorizing key angles.

BeautifulLight
Messages
39
Reaction score
0
Solving for Sin with no calculator + additional questions

Untitled.jpg


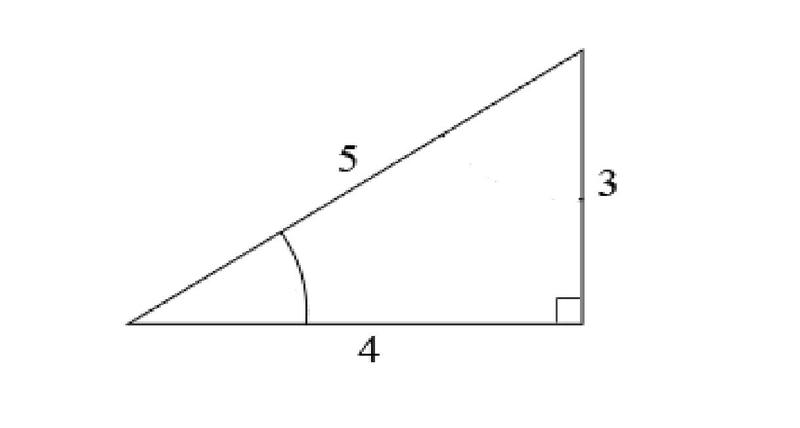
Sinθ=opp/hyp

Sinθ=5/3

Sinθ=1.6


I know the answer is 35.87°. I would like to convert 1.6 to 35.87° but am unsure how.
 
Last edited:
Mathematics news on Phys.org
BeautifulLight said:
View attachment 72721

Sinθ=opp/hyp

Sinθ=5/3

Sinθ=1.6


I know the answer is 35.87°. I would like to convert 1.6 to 35.87° but am unsure how.

Sinθ=3/5=0.6. You need a calculator or sine table.
 
mathman said:
Sinθ=3/5=0.6. You need a calculator or sine table.

Oops!

It's impossible to figure out? I am trying to prepare myself for the Accuplacer exam. Calculators are not allowed.
 
This is not an angle that any reasonable person would expect you to know the sine, cosine, or other trig functions for. So finding that angle means that you'll need to use something to get an approximation; i.e., a calculator or table of trig functions.

A more serious problem is that you misused the formula and calculated hyp/opp, instead of opp/hyp. Also, getting a value larger than 1 for the sine of an angle should have been a red flag. The values of sine and cosine are always between -1 and +1 for real number angles.
 
It's a 3-4-5 triangle. Might someone have suggested memorization of its Pythagorean Triple angles, similar to memorizing the unit circle functions?
 
Doug Huffman said:
It's a 3-4-5 triangle. Might someone have suggested memorization of its Pythagorean Triple angles, similar to memorizing the unit circle functions?
Not that I've seen in numerous precalc/trig textbooks. The usual angles to be memorized are 0°, 30°, 45°, 60°, and 90°, along with their counterparts in the other three quadrants.
 

Similar threads

High School Confusion about the angle between two vectors in a cross product
  • · Replies 7 ·
Replies
7
Views
3K
High School Why does the trigonometry of obtuse angles use ref angles?
  • · Replies 10 ·
Replies
10
Views
2K
Find ratio of brightness & the distance the 6th dark fringe is from central fringe
  • · Replies 5 ·
Replies
5
Views
906
Undergrad How do I do this calculation involving the SIN function?
  • · Replies 9 ·
Replies
9
Views
2K
High School How Can Trigonometry Calculate Distances in Surveying?
  • · Replies 5 ·
Replies
5
Views
3K
High School What do the Trigonometic functions mean?
  • · Replies 2 ·
Replies
2
Views
2K
AP Physics C Mechanics: Linear Momentum for Colliding Billiard Balls
  • · Replies 4 ·
Replies
4
Views
2K
Solving Reciprocal Trigonometric Equation cot^2θ+5cosecθ=4
  • · Replies 13 ·
Replies
13
Views
2K
High School Compound Angle Formula: Solving Double Angle Equations
  • · Replies 5 ·
Replies
5
Views
1K
High School Need an on-line calculator for a simple calculation
  • · Replies 12 ·
Replies
12
Views
4K