Solving for v_1, v_2, and v_3 with Nodal Analysis

[VinnyCee]

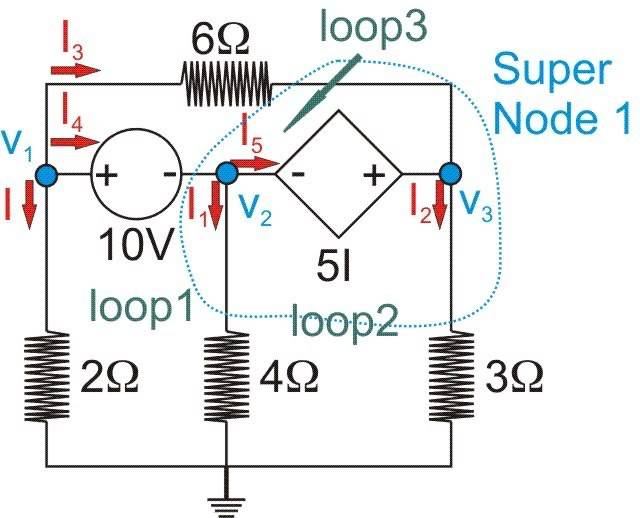
Find $v_1,\,v_2,\,and\,v_3$ in the circuit below using nodal analysis:

My work so far:

$$I\,=\,\frac{v_1}{2\Omega},\,\,I_1\,=\,\frac{v_2}{4\Omega},\,\,I_2\,=\,\frac{v_3}{3\Omega},\,\,I_3\,=\,\frac{v_1\,-\,v_3}{6\Omega}$$

KVL @ loop1 => $$-I\,(2\Omega)\,+\,10\,V\,+\,I_1(4\Omega)\,=\,0$$

Which equals:
$$-\left(\frac{v_1}{2\Omega}\right)(2\Omega)\,+\,10\,V\,+\,\left(\frac{v_2}{4\Omega}\right)(4\Omega)\,=\,0$$

Which equals:
$$-v_1\,+\,10\,V\,+\,v_2\,=\,0$$

KVL @ loop2 => $$-v_2\,-\,5\,I\,+\,v_3\,=\,0$$

KVL @ loop3 => $$-10\,V\,+\,v_1\,-\,v_3\,+\,5\,I\,=\,0$$

KCL @ v1 => $$I\,+\,I_3\,+\,I_4\,=\,0$$

KCL @ v2 => $$I_4\,=\,I_1\,+\,I_5$$

KCL @ v3 => $$I_2\,=\,I_5\,+\,I_3$$

KCL @ Super Node 1 => $$I_4\,+\,I_3\,=\,I_1\,+\,I_2$$

When I combine these equations to get 4 equations with 4 variables, I get the following matrix:

$$\left[\begin{array}{cccc|c}<br /> -1 & 1 & 0 & 0 & -10 \\<br /> 0 & -1 & 1 & -5 & 0 \\<br /> 1 & 0 & -1 & 5 & 10 \\<br /> \frac{1}{2} & \frac{1}{4} & \frac{1}{3} & 0 & 0<br /> \end{array}\right]$$

The columns go like this: v1, v2, v3, I, constant

But this matrix has infinite solutions! How do I solve?

 

[VinnyCee]

I figured it out!

The last variable column of the matrix can be eliminated because $$I\,=\,\frac{v_1}{2\Omega}$$

This gives the matrix:

$$\left[\begin{array}{ccc|c}-1 & 1 & 0 & -10 \\-\frac{5}{2} & -1 & 1 & 0 \\ \frac{7}{2} & 0 & -1 & 10 \\ \frac{1}{2} & \frac{1}{4} & \frac{1}{3} & 0 \end{array}\right]$$

This RREF's out to:

$$v_1\,=\,\frac{70}{23}\,=\,3.043\,V$$

$$v_2\,=\,-\frac{160}{23}\,=\,-6.956\,V$$

$$v_3\,=\,\frac{15}{23}\,=\,0.6522\,V\,V$$

NOTE: The third row of the matrix is not required!