asi123
- 254
- 0
Homework Statement
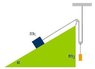
\alpha = 37, m1 = 10 kg
Also attachment.
Homework Equations
The Attempt at a Solution
ok, the first question is to find m2 when the system is in rest and the second one is to find the acceleration when m1 = m2.
I found 3 equations:
n1 = m1 * g * cos(\alpha )
m1 * g * sin(\alpha ) = T2
T1 + T2 = m2 * g
I need another one I think...
Could it be that T1 = T2?
And as for the second one, how can I find the equations between the accelerations? (there is always one...)
10x in advance.