Jacob87411
- 170
- 1
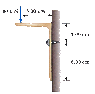
A shelf bracket is mounted on a vertical wall by a single screw, as shown in Figure P12.59. Neglecting the weight of the bracket, find the horizontal component of the force that the screw exerts on the bracket when an F = 86.0 N vertical force is applied as shown.
Ok so we have three equations like usual with statics.
Forces in Y = 86N-Fb=ma
Forces in X = 0=ma
Torque=0 so (86)(.05)-(Fb)(.03)=0
Taking the point of rotation at the top right corner of the bracket, 3cm above the screw.
Fb=Force of the bracket
Or do you solve for Fb in the torque equation giving Fb=143.33 then find its X and Y components. The Y would be 86, then the X would be 57.33?
I guess what I am confused by is why there is an X force from the screw and how to find it
Ok so we have three equations like usual with statics.
Forces in Y = 86N-Fb=ma
Forces in X = 0=ma
Torque=0 so (86)(.05)-(Fb)(.03)=0
Taking the point of rotation at the top right corner of the bracket, 3cm above the screw.
Fb=Force of the bracket
Or do you solve for Fb in the torque equation giving Fb=143.33 then find its X and Y components. The Y would be 86, then the X would be 57.33?
I guess what I am confused by is why there is an X force from the screw and how to find it
Attachments
Last edited: