BOAS
- 546
- 19
Hi,
i'm stuck on this problem and have been trying to identify where I might have made an error but have come up empty. I have assigned my loops and junctions and have three equation for three unknowns, but can't seem to solve them...
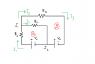
Consider the circuit in the following diagram (attached):
where the two ideal dc batteries deliver a terminal voltage of V1 = 2V and V2 = 10V respectively. The magnitude of the resistances is R1 = 2Ω; R2Ω = 2; and R3 = 3Ω. Calculate the magnitude and direction of the current across the resistor R2.
Kirchhoff's junction and loop rule.
I1 = I2 + I3 (JR)
v1 - I1R1 - I2R2 = 0 (loop A)
-I3R3 + V2 + I2R2 = 0 (loop B)
I can't see how to solve for any of these, which is making me think I've worked out the expressions wrong, but I can't find the mistake.
Thanks for any help you can give,
BOAS
i'm stuck on this problem and have been trying to identify where I might have made an error but have come up empty. I have assigned my loops and junctions and have three equation for three unknowns, but can't seem to solve them...
Homework Statement
Consider the circuit in the following diagram (attached):
where the two ideal dc batteries deliver a terminal voltage of V1 = 2V and V2 = 10V respectively. The magnitude of the resistances is R1 = 2Ω; R2Ω = 2; and R3 = 3Ω. Calculate the magnitude and direction of the current across the resistor R2.
Homework Equations
Kirchhoff's junction and loop rule.
The Attempt at a Solution
I1 = I2 + I3 (JR)
v1 - I1R1 - I2R2 = 0 (loop A)
-I3R3 + V2 + I2R2 = 0 (loop B)
I can't see how to solve for any of these, which is making me think I've worked out the expressions wrong, but I can't find the mistake.
Thanks for any help you can give,
BOAS